The capillary pressure functions 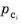 can be supplied as user defined expressions, or, in case there are only two phases present in the Phase Transport in Porous Media
can be supplied as user defined expressions, or, in case there are only two phases present in the Phase Transport in Porous Media interface, the capillary pressure function can be derived from van Genuchten (
Ref. 1) or Brooks and Corey (
Ref. 2) models. When either of these predefined models is used, the user has to specify which phase is the wetting phase. If the wetting phase is the same as the phase computed from the volume constraint, then
where pec is the entry capillary pressure and
mvG is a constitutive constant, and where
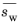
denotes the effective saturation of the wetting phase. The effective saturation of each phase is defined as
where srj denotes the residual saturation of phase
j. For the Brooks and Corey model, the capillary pressure curve depends on saturation as
where λp is the pore distribution index.
where mvG and
lvG are constitutive constants, and where
sn denotes the volume fraction of the nonwetting phase. For the Brooks and Corey model, the relative permeabilities are given by
where λp is again the pore distribution index.
where 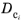 denotes the capillary diffusion coefficient for phase i.
denotes the capillary diffusion coefficient for phase i. The volumetric flux for the phases not computed from the volume constraint is in this case given by