where the quantity λ (SI unit: N) is the mixing energy density and
ε (SI unit: m) is a capillary width that scales with the thickness of the interface. These two parameters are related to the surface tension coefficient,
σ (SI unit: N/m), through the equation
and γ is the mobility parameter which is related to
ε through
γ = χε2 where
χ is the mobility tuning parameter (set to 1 by default). The volume fractions of Fluid 1 and Fluid 2 are computed as
where the min and
max operators are used so that the volume fractions have a lower limit of
0 and an upper limit of
1. Let
ρ1 and
ρ2 be the constant densities of Fluid 1 and Fluid 2, respectively. When
Density averaging is set to
Volume average, the density is defined as,
switching to Heaviside function, the density is defined as,
where H is a smooth step function and
lρ is a mixing parameter defining the size of the transition zone. When the
Harmonic volume average is selected,
where μ1 and
μ2 are the dynamic viscosities of Fluid 1 and Fluid 2, respectively.
where G is the chemical potential defined as:
where G is the chemical potential (SI unit: J/m
3) defined in
The Equations for the Phase Field Method and
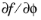
is a user-defined source of free energy.
-derivative of the external free energy has been defined in the External Free Energy section of the Fluid Properties feature.