Note that Equation 6-4, and
Equation 6-5 are solved in the contained interface,
Laminar Flow or
Turbulent Flow interface. Note that the form of the continuity equation, appropriate for high density difference mixtures, differs from the definition in
Theory for the Single-Phase Flow Interfaces.
where γ is the reinitialization parameter (set to 1 by default), and
ε is the interface thickness controlling parameter (set to
hmax/2 where
hmax is the maximum element size in the component). The density is a function of the level set function. Let
ρ1 and
ρ2 be the constant densities of Fluid 1 and Fluid 2, respectively. Here, Fluid 1 corresponds to the domain where
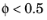
, and Fluid 2 corresponds to the domain where
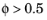
. When
Density averaging is set to
Volume average, the density is defined as,
switching to Heaviside function, the density is defined as,
where H is a smooth step function and
lρ is a mixing parameter defining the size of the transition zone. When the
Harmonic volume average is selected,
where μ1 and
μ2 are the dynamic viscosities of Fluid 1 and Fluid 2, respectively. For inelastic non-Newtonian fluids,
μ1,2 is replaced by
μapp1,2 in the previous expressions. Further details of the theory for the level set method are in
Ref. 1.
where the quantity λ (SI unit: N) is the mixing energy density and
ε (SI unit: m) is a capillary width that scales with the thickness of the interface. These two parameters are related to the surface tension coefficient,
σ (SI unit: N/m), through the equation
and γ is the mobility parameter which is related to
ε through
γ = χε2 where
χ is the mobility tuning parameter (set to 1 by default). The volume fractions of Fluid 1 and Fluid 2 are computed as
where the min and
max operators are used so that the volume fractions have a lower limit of
0 and an upper limit of
1. Let
ρ1 and
ρ2 be the constant densities of Fluid 1 and Fluid 2, respectively. When
Density averaging is set to
Volume average, the density is defined as,
switching to Heaviside function, the density is defined as,
where H is a smooth step function and
lρ is a mixing parameter defining the size of the transition zone. When the
Harmonic volume average is selected,
where μ1 and
μ2 are the dynamic viscosities of Fluid 1 and Fluid 2, respectively. For inelastic non-Newtonian fluids,
μ1,2 are replaced by
μapp1,2 in the previous expressions.
where G is the chemical potential defined as:
The four forces on the right-hand side of Equation 6-4 are due to gravity, surface tension, a force due to an external contribution to the free energy (using the phase field method only), and a user-defined volume force.
where σ is the surface tensions coefficient (SI unit: N/m),
n is the unit normal to the interface, and
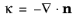
is the curvature.
δ (SI unit: 1/m) is a Dirac delta function located at the interface.
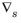
is the surface gradient operator
The δ-function is approximated by a smooth function according to
where G is the chemical potential (SI unit: J/m
3) defined in
The Equations for the Phase Field Method and
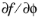
is a user-defined source of free energy. When
Shift surface tension force to the heaviest phase is selected the surface-tension force is added as,
where ds,Fst is a smoothing factor. This can be used to avoid unphysical acceleration of a light phase near a phase interface caused by the smearing of the phase interface across a few mesh cells.
If Include surface tension gradient effects in surface tension force is selected, extra terms are added to account for the Marangoni effect due to gradients in the surface tension coefficient (see
Ref. 6):
The gravity force is Fg =
ρg where
g is the gravity vector. Add this as a Gravity feature to the fluid domain.
-derivative of the external free energy has been defined in the External Free Energy section of the Fluid Properties feature.