The Mixture Model, Laminar Flow Interface

The interface (

), found under the branch (

) when adding a physics interface, is used to model the flow at low and moderate Reynolds numbers of liquids containing a dispersed phase. The dispersed phase can be bubbles, liquid droplets, or solid particles, which are assumed to always travel with their terminal velocity.

The Mixture Model, Laminar Flow interface solves one set of Navier–Stokes equations for the momentum of the mixture. The pressure distribution is calculated from a mixture-averaged continuity equation and the velocity of the dispersed phase is described by a slip model. The volume fraction of the dispersed phase is tracked by solving a transport equation for the volume fraction.

The physics interface can also model the distribution of the number density, which in turn can be used to calculate the interfacial area, which is useful when simulating chemical reactions in the mixture.

The main physics node is the Mixture Properties feature. It adds the equations for the mixture and provides an interface for defining the fluid materials for the continuous and dispersed phases as well as which slip model and mixture viscosity model to use.

When this physics interface is added, the following default physics nodes are also added in the — , , and . Then, from the toolbar, add other nodes that implement, for example, boundary conditions and volume forces. You can also right-click to select physics features from the context menu.

The is the default physics interface name.

The is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern <name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the name string must be unique. Only letters, numbers, and underscores (_) are permitted in the field. The first character must be a letter.

The default (for the first physics interface in the model) is mm.

Specify the characteristics of the dispersed phase, the model for the slip velocity, and whether or not to solve for the interfacial area.

To characterize the , select (the default) or .

The selection from this list is further defined for the Mixture Properties node under the Mixture Model section.

To compute the slip velocity jslip (SI unit: m/s), select a — (the default), , , , or .

•

The model assumes that the velocities of the two phases are equal, that is, uslip = 0.

•

For specify an arbitrary expression for the relative velocity. For example, give a constant velocity based on experimental data. Enter the uslip (SI unit: m/s) or jslip (SI unit: m/s) in the Mixture Properties node under the Mixture Model section.

To add a transport equation for the number density of the dispersed particles, in order to determine the interfacial area, select the check box (by default not selected).

For the Mass Transfer rate, use a two-film theory model, which includes the interfacial area per unit volume between the two phases. It is possible to compute the interfacial area per unit volume if the number density n (that is, the number of dispersed particles per volume) is known. Select the check box to add the following equation for the number density n:

This equation states that a dispersed phase particle cannot disappear, appear, or merge with other particles, although it can expand or shrink.

The Mixture Model, Laminar Flow Interface calculates the interfacial area a (SI unit: m2/m3) from

Reference values are global quantities used to evaluate the density of both phases and the absolute pressure pA.

There are generally two ways to include the pressure in fluid flow computations: either to use the absolute pressure pA = p + pref, or the gauge pressure p. When pref is nonzero, the physics interface solves for the gauge pressure whereas material properties are evaluated using the absolute pressure. The reference pressure level is also used to define the density of both phases. The default pref (SI unit: Pa) is 1[atm].

The reference temperature is used to define the density of both phases. The default Tref (SI unit: K) is 293.15[K].

For 2D axisymmetric components, select the check box to include the swirl velocity component — that is, the velocity component

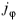
in the azimuthal direction. While

can be nonzero, there can be no gradients in the

direction

	General Single-Phase Flow Theory

The default selection is .

Enter values for the dependent variables (field variables):

The names can be changed but the names of fields and dependent variables must be unique within a component.

	In previous versions of COMSOL Multiphysics (prior to version 5.4), the Mixture Model interfaces solved for the mass-averaged mixture velocity u. Now, the volume-averaged mixture velocity j is used. For specific details, see Theory for the Mixture Model Interfaces and Mass-Averaged Mixture Velocity.

To display this section, click the button (

) and select in the dialog box.

The consistent stabilizations and are by default applied to the . In addition, when the flow is turbulent, the consistent stabilizations are also applied to the . Additional inconsistent stabilization terms may be added when required as isotropic diffusion.

To display this section, click the button (

) and select in the dialog box. Normally these settings do not need to be changed.

can be used to suppress negative values of the dispersed volume fraction. Including this term has been observed to slow down convergence and it is therefore disabled by default.

Select the check box to add pseudo time derivatives to the equation when the form is used. When selected, also choose a — (the default) or . sets the local CFL number (from the Courant–Friedrichs–Lewy condition) to the built-in variable CFLCMP which in turn triggers a PID regulator for the CFL number. For enter a CFLloc (dimensionless).