The Convected Wave Equation, Time Explicit (cwe) interface (), found under the Acoustics>Ultrasound subbranch () when adding a physics interface, is used to solve large transient linear acoustic problems containing many wavelengths in a stationary background flow. It is suited for time-dependent simulations with arbitrary time-dependent sources and fields. In general, the interface is suited for modeling the propagation of acoustic signals over large distances relative to the wavelength, for example, linear ultrasound problems. Application areas include ultrasound flowmeters and other ultrasound sensors where time of flight is an important parameter. The applications are not restricted to ultrasound. The interface includes absorbing layers that are used to set up effective nonreflecting like boundary conditions.The interface exists in 2D, 2D axisymmetric, and 3D.

In the no-flow case it can be advantageous to use The Pressure Acoustics, Time Explicit Interface instead. The equations are the same but the latter interface has more options to, for example, model scattering phenomena using a scattered field formulation; or for handling sharp material discontinuities.

For modeling acoustic-structure interaction (ASI) or vibroacoustic problems the interface is fully multiphysics enabled and can be coupled to the The Elastic Waves, Time Explicit Interface, using either the Convected Acoustic-Structure Boundary, Time Explicit or the Pair Convected Acoustic-Structure Boundary, Time Explicit multiphysics couplings.

The interface solves the linearized Euler equations assuming an adiabatic equation of state. The dependent variables are the acoustic pressure p and the acoustic velocity perturbation u. The background mean flow can be any stationary flow with small to moderate velocity gradients. General bulk dissipation (volumetric damping) can be added to model real fluids.

When this physics interface is added, these default nodes are also added to the Model Builder — Convected Wave Equation Model, Sound Hard Wall, Initial Values, and Axial Symmetry (in case of 2D axisymmetric). Then, from the Physics toolbar, add other nodes that implement, for example, boundary conditions. You can also right-click Convected Wave Equation, Time Explicit to select physics features from the context menu.

The Label is the default physics interface name.

The Name is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern <name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the name string must be unique. Only letters, numbers, and underscores (_) are permitted in the Name field. The first character must be a letter.

The default Name (for the first physics interface in the model) is cwe.

To display this section, click the Show More Options button () and select Advanced Physics Options in the Show More Options dialog box. In the Filter Parameters for Absorbing Layers section you can change and control the values set for the filter used in the Absorbing Layers. The values of the filter parameters defined here are used in all absorbing layers added to the model and they override the value of filter parameters enabled in the material model (Convected Wave Equation Model). The default values of the filter parameters α, ηc, and s are set to 0.1, 0.01, and 2, respectively. Inside the absorbing layer it is important to use a filter that is not too aggressive since this will result in spurious reflections.

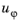
This section is only available in 2D Axisymmetric. Per default the acoustic velocity perturbation u is assumed to have only two components: the radial component ur and the axial component uz. You can select the Include out-of-plane components check box to enable the third — circumferential component , which physically can only be nonzero if the background mean flow has the corresponding component.

In this section you can select the discretization for the Acoustic pressure and Acoustic velocity. Per default both are set to Quartic (4th order). Using quartic elements together with a mesh size equal to approximately half the wavelength to be resolved, leads to the best performance when using the dG method. For further details see the Meshing, Discretization, and Solvers section.

The dependent variables (field variables) are the Acoustic pressure, Acoustic velocity, and Acoustic velocity, components. The names can be changed, but the names of fields and dependent variables must be unique within a model.