For the sake of brevity, consider the 1D Equation 2-58. In order to derive the PML formulation in the time domain, the following steps are taken (
Ref. 39). First, consider a special form of the mapping
Equation 2-57:
Then, taking Equation 2-59 into account, multiply
Equation 2-58 by
1+σ(x)/iω.
Equation 2-58 transforms to the following form:
Equation 2-60 and
Equation 2-61 yield a system of partial differential equations in the time domain equivalent to the frequency domain
Equation 2-58:
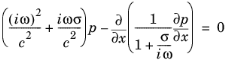 .
.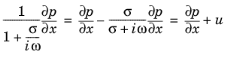 .
.