The resulting value of Zn can be treated as a superposition of several contributions which are derived separately. Note that the theory below is only valid for the perforates with circular-shaped holes. Other types of holes can lead to significantly different results, which will make the models that are considered here inadequate and unreliable.

Let the z-coordinate axis be directed along the axis of a cylindrical hole of the height tp (see Figure 2-15). Let the variation of the pressure and the velocity along the z-axis have the following pattern:

The substitution of Equation 2-36 into Equation 2-35 results in

where Zc is the characteristic impedance and kc is the complex wave number defined according to the low reduced frequency (LRF) models from the Narrow Region Acoustics for Slits, Circular Ducts, Rectangular Ducts, and Equilateral triangular Ducts. That is,

Note that Equation 2-38 coincides with the expression that follows from Crandall’s formula for an infinite tube with the circular cross section (see Ref. 35). Equation 2-37 accounts for both viscous and thermal effects inside the hole, while the simplified Equation 2-38 contains the viscous part only (thermal effects are negligible for the thin plate limit).

Equation 2-37 and Equation 2-38 are exact if the streamlines of a flow through the hole are parallel to the z-axis throughout the orifice area. In reality, there is a radial component of the flow, which leads to the reduction (contraction) of this area. The minimum area where the streamlines remain parallel to the z-axis is called vena contracta. The flow velocity at the vena contracta is also different from that of the ideal flow. A coefficient that accounts for these effects is called the discharge coefficient, CD. The value of the discharge coefficient can be obtained from measurements as function of the plate thickness and the orifice shape and diameter.

Another parameter that used to express the interior impedance of a perforate is the porosity, σ. The holes are usually uniformly distributed over the plate, and the porosity accounts for the distribution as the ratio of the hollow area to the area of the plate. Depending on the pattern used when the holes are strewn over the plate, the porosity is defined as follows

for a square and a triangular pattern, respectively. The parameter a determines the hole spacing.

The resulting expression for the interior impedance of a perforate comes out from dividing zi by the product σCD:

Either Equation 2-37 or Equation 2-38 can be used for the substitution for zi in Equation 2-39. The resulting models will further be referred to as the thick and the thin plate models, respectively.

The subscript “orifice” in Equation 2-39 means that the expression accounts for the transfer impedance of a perforate caused by the presence of the holes; that is, a piston of fluid of the length tp. However, the actual mass of fluid affected by an incident wave is larger than that inside the hole. The effective mass of the fluid can be taken into account by the piston which is on each side longer by δ than the initial one (see Figure 2-16). This results in adding two extra terms (for each side of the perforate) of the form Equation 2-38 with tp replaced by δ. The choice of Equation 2-38 is due to the absence of highly conducting walls in the end corrections area.

If two holes are located relatively close to one another, the actual masses of the attached fluid can become overlapped. This makes the total mass less than just the sum of those for the separate hole. In order to take the hole-hole interaction into account, the end correction is reduced by a factor fint.

The end correction is usually considered as a function of the hole diameter and can in practice be different for the resistive and the reactive parts of the transfer impedance. For this reason, it is useful to split δ into two parts: δresist and δreact. The resulting term that accounts for the end correction and the hole-hole interaction reads

At medium and high sound pressure levels, the displacement of acoustic particles becomes comparable to the diameter of the holes. This causes flow separation and vortex shedding at the entrance and the exit of the hole. This results in the acoustic energy dissipation and increases the acoustic resistance of the perforate Ref. 36. That is, an extra resistance term should be added to the resulting transfer impedance expression.

where fnl is a correction factor (equals 1 by default) and vn is the acoustic particle velocity component normal to the plate. Other expressions for the nonlinear resistance term can be found in Ref. 36.

Relative to the mean flow, the contribution of a grazing or a bias flow to the resistance can be expressed through the flow Mach number as shown in Ref. 37.

Combining the expressions Equation 2-39–Equation 2-42 together yields the full expression for the transfer impedance of a perforate for the thick

plate models. The discharge coefficient CD is taken different for the linear and the nonlinear parts for the sake of flexibility.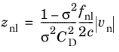