Mathematically, a specific acoustic impedance Zn is defined on some cross section as the ratio between the acoustic pressure
p and the acoustic velocity perpendicular to the area
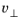
(the normal velocity)
Here Zn is the specific acoustic (input) impedance of the external domain and it has the unit of a specific acoustic impedance. The specific acoustic impedance
Zn (SI unit: Pa·s/m) is related to the acoustic impedance
Zac (ratio of pressure and flow rate, SI unit: Pa·s/m
3) and the mechanical impedance
Zmech (ratio of force and velocity, SI unit: N·s/m) via the area
A of the boundary, according to