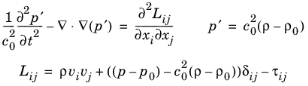In Lighthill’s seminal work (Ref. 63 and
Ref. 64) he transformed (rearranged) the full set of Navier–Stokes equations (momentum and mass conservation) into an inhomogeneous wave equation. The source term of the wave equation only being important within turbulent flow regions and thus representing the flow-induced noise source. The equation is given by
where Lij is called the Lighthill stress tensor,
c is the speed of sound,
p is the pressure (total),
ρ is the density (total),
τij is the viscous stress tensor, and the subscript 0 refers to the reference properties of the fluid at rest. It is assumed that
p’ represents the linear acoustic pressure variations outside of the source domain. The Lighthill stress tensor consists of three contributing parts (see
Ref. 65): the Reynolds stress (first term), a term containing the excess pressure generated by nonlinear processes and compressibility effects in the moving fluid (second term), and the viscous stress tensor that accounts for attenuation of the sound (third term).
This is the expression for the source term stress tensor used when the Acoustic analogy option is set to
Lighthill. The viscous dissipation can optionally be included by selecting
Include viscous stress. This is a symmetric tensor that contains 9 elements in 3D of which 6 are unique.
The Lighthill wave equation can be further approximated at low Mach numbers for an incompressible flow (see Ref. 65,
67, and
68). This leads to a simplified inhomogeneous wave equation known as the
aeroacoustic wave equation or AWE, given by
where p is the linear acoustic pressure fluctuation and
pic is the pressure variation associated with the incompressible flow simulation. This equation is solved (in the frequency domain) when the he
Acoustic analogy option is set to
Aeroacoustic wave equation. In the
Aeroacoustic Flow Source the right hand side is included as the Fourier components of the second time derivative of the incompressible flow variation,
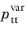
in the
Equation section.