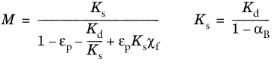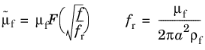Poroelastic Material

Use the node to define the poroelastic material and fluid properties, that is the properties of the porous matrix and the saturating fluid.The subnode is available from the context menu (right-click the parent node) or from the toolbar, menu.

•

, this model is primarily used in earth sciences when the saturating fluid is a liquid like water or oil. The model is based on Biot’s original work and only includes the effects of viscous losses in the pores.

•

, this model is intended for simulating porous materials where the saturating fluid is air. This is for modeling sound absorbers, liners, foams used in headphones and loudspeakers, cloth and much more.

	Three different waves can propagate in a poroelastic material; fast pressure waves, slow pressure waves, and shear waves. Their speed can be evaluated through the variables pelw.cp_fast, pelw.cp_slow, and pelw.cs_poro, respectively. These should not be confused with the material properties for the constituting solid (pelw.cp and pwel.cs) and fluid (pelw.c). All three poroelastic wave types should be resolved by the computational mesh.

The default uses the (the material defined for the domain). This setting should be different from the one for the selected in the section. Typically, select another material directly (a material defined in the node) for the porous elastic material and use the default option for the .

Select a : ; ; or . Then enter or select the settings as described.

If is selected from the list, select a pair of elastic properties to describe an isotropic drained porous material. The drained parameters are also sometimes referred to as the in vacuo elastic parameters; they are in principle measured without the presence of the saturating fluid. From the list, select:

•

to specify drained Young’s modulus (elastic modulus) Ed (SI unit: Pa) and Poisson’s ratio νd (dimensionless). For an isotropic material, Young’s modulus is the spring stiffness in Hooke’s law, which in 1D form is σ = Edε, where σ is the stress and ε is the strain. Poisson’s ratio defines the normal strain in the perpendicular direction, generated from a normal strain in the other direction and follows the equation ε⊥ = −υε||

•

(the default for the Biot-Allard model) to specify drained shear modulus Gd (SI unit: Pa) and Poisson’s ratio νd (dimensionless).

•

to specify drained Young’s modulus (elastic modulus) Ed (SI unit: Pa) and drained shear modulus Gd (SI unit: Pa).

•

(the default for the Biot model) to specify the drained bulk modulus Kd (SI unit: Pa) and the drained shear modulus Gd (SI unit: Pa). The bulk drained modulus is a measure of the solid porous matrix’s resistance to volume changes. The shear modulus is a measure of the solid porous matrix’s resistance to shear deformations.

•

to specify the drained pressure-wave speed cp (SI unit: m/s) and the shear-wave speed cs (SI unit: m/s).

For each pair of properties, select from the applicable list to use the value or enter a value or expression. Each of these pairs define the drained elastic properties and it is possible to convert from one set of properties to another.

When is selected from the list, the material properties of the solid porous matrix vary in orthogonal directions only.

The default properties take values . For , enter values or expressions for the drained E (SI unit: Pa), the drained ν (dimensionless), and the drained G (SI unit: Pa).

When is selected from the list, the material properties of the solid porous matrix vary in all directions, and the stiffness comes from the symmetric , D (SI unit: Pa). The default uses values . For enter values in the 6-by-6 symmetric matrix that displays.

Enter the following (remaining) parameters necessary to define the properties of a porous material model. The defaults use values . For enter other values or expressions as needed.

•

(the default for the Biot model as described above) to specify the drained bulk modulus Kd (SI unit: Pa) and the drained shear modulus Gd (SI unit: Pa).

•

to specify the drained density of the porous material in vacuum ρd (SI unit: kg/m3). The drained density ρd is equal to (1 − εp) ρs where ρs is the density of the solid material from which the matrix is made and εp is the porosity.

•

to specify the permeability of the porous material κp (SI unit: m2). The permeability is a measure of the ability of the porous material to let fluid pass through it. It hence gives some measure of the pore size and thus correlates to the viscous damping experienced by pressure waves propagating in the saturating fluid.

•

to specify the porosity of the material εp (dimensionless). It defines the amount of void volume inside the porous matrix and takes values between 0 (no porous material only fluid) and 1 (fully solid material no fluid).

•

to specify the Biot-Willis coefficient αB (dimensionless). This coefficient relates the bulk modulus (compressibility) of the drained porous matrix to a block of solid material. It is defined as

where Kd is the drained bulk modulus and Ks is the bulk module of a block of solid material (made of the matrix material). The drained bulk modulus is related to the stiffness of the porous matrix, while the solid bulk modulus is related to the compressibility of the material or grains from which the porous matrix is made. The Biot-Willis coefficient is bound by

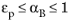
. A rigid porous matrix (Voigt upper bound) has αB = εp and a soft or limp porous matrix (Reuss lower bound) has αB = 1.

•

(high frequency limit) or the structural form factor

(dimensionless). This is a purely geometrical factor that depends on the microscopic geometry and distribution of the pores inside the porous material. It is independent of the fluid and solid properties and is normally >1. The default is 2. The more complex the propagation path through the material, the higher is the absorption. The tortuosity partly represents this complexity.

Enter the following (remaining) parameters necessary to define the properties of a porous material model. The defaults use values . For enter other values or expressions as needed.

•

(the default for the Biot-Allard model as described above) to specify drained shear modulus Gd (SI unit: Pa) and Poisson’s ratio νd (dimensionless).

•

to specify the (static) flow resistivity of the porous material Rf (SI unit: Pa·s/m2). The flow resistivity is a measure of the ability of the porous material to let fluid pass through it. It hence gives some measure of the pore size and thus correlates to the viscous damping experienced by pressure waves propagating in the saturating fluid. The flow resistivity is also sometimes denoted σ (using the unit N·s/m4) and it is related to the permeability through κp = μ/Rf.

•

to specify the loss factor of the porous matrix ηs (dimensionless). This value introduces the damping due to losses in the porous structure by transform the elastic moduli into complex valued quantities. This quantity can be frequency dependent if necessary.

•

(high frequency limit) or the structural form factor τ∞ (dimensionless). This is a purely geometrical factor that depends on the microscopic geometry and distribution of the pores inside the porous material. It is independent of the fluid and solid properties and is normally >1. The default is 2. The more complex the propagation path through the material, the higher the absorption. The tortuosity partly represents this complexity.

•

to specify the viscous length scale Lv (SI unit: m). This value is sometimes denoted Λ and replaces the hydraulic radius used in simpler models to account for the viscous losses that appear in the acoustic boundary layer at pore walls.

•

to specify the thermal length scale Lth (SI unit: m). This value is sometimes denoted Λ’ and replaces the hydraulic radius used in simpler models to account for the thermal losses that appear in the acoustic boundary layer at pore walls.

•

how to calculate the Biot–Willis coefficient αB by selecting , (the default), , or . This coefficient relates the bulk modulus (compressibility) of the drained porous matrix to a block of solid material.

where Kd is the drained bulk modulus and Ks is the bulk module of the skeleton material (bulk modulus of a block of solid material made of the matrix material). When this option is selected also enter the Ks (taken from material as default). The drained bulk modulus Kd is related to the stiffness of the porous matrix, while the skeleton bulk modulus Ks is related to the compressibility of the material or grains from which the porous matrix is made. The Biot–Willis coefficient is bound by

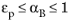
. A rigid porous matrix (Voigt upper bound) has αB = εp and a soft or limp porous matrix (Reuss lower bound) has αB = 1.

enter a value for the Biot-Willis coefficient αB (dimensionless). In the limp limit when αB = 1 it is recommended to use the Poroacoustics feature of The Pressure Acoustics, Frequency Domain Interface instead of the Poroelastic Waves interface. In poroacoustics the limp limit, when the structure is so “fluffy” that it moves with the fluid, has the assumption Kd = 0 and αB = 1 included explicitly.

•

to define the dynamic viscosity of the saturating fluid μf (SI unit: Pa·s). The parameter is important for the amount of viscous damping experienced by the acoustic waves.

•

of the saturating fluid χf (SI unit: 1/Pa). Remember that the fluid compressibility χf is related to the fluid bulk modulus Kf (SI unit: Pa) and the speed of sound c, through the relation

It should be noted that Biot-Willis coefficient αB only depends on the properties of the porous matrix while Biot’s module M depends on both fluid and porous matrix properties.

•

models damping at low frequencies where the acoustic boundary layer (the viscous penetration depth) is assumed to span the full width of the pores. This is also the so-called Poiseuille limit.

•

For also select as or . Either enter a fr (SI unit: Hz) or a a (SI unit: m). This model implements a correction factor to the viscosity that accounts for the relative scale difference between a typical pore diameter and the acoustic boundary layer thickness. The modified viscosity is of the form

where fr is the reference frequency and a is a characteristic size of the pores. The expression for fr is one typically used in literature but it is often measured or empirically determined. The expression for fr corresponds to finding the frequency at which the viscous boundary layer thickness is of the scale a.

	See High Frequency Correction (Biot Model) for more details.

•

to define the dynamic viscosity of the saturating fluid μf (SI unit: Pa·s). The parameter is important for the amount of viscous damping experienced by the acoustic waves.

•

to define the (specific) heat capacity at constant pressure of the saturating fluid Cp (SI unit: J/(kg·K)).

•

to define the thermal conductivity of the saturating fluid k (SI unit: W/(m·K)). The parameter is important for the amount of thermal damping experienced by the acoustic waves.