You are viewing the documentation for an older COMSOL version. The latest version is
available here.
A prerequisite for setting up the mechanical contact problem is to define the contact search between the source boundary and the destination boundary. The purpose of the search is to detect points on the contacting boundaries that are in contact or may come in contact, and also to map quantities between such points. This part of the contact problem is defined in the Contact Pair that sets up relevant variables and operators to map quantities between the selected source and destination boundaries. In COMSOL Multiphysics, the contact search is made using a ray-tracing strategy as depicted in
Figure 3-34. For mechanical contact, most variables and equations are formulated on the destination boundary. Hence, the typical mapping of interest here is from the source boundary to the destination boundary, however, it is possible to map quantities in the opposite direction as well.
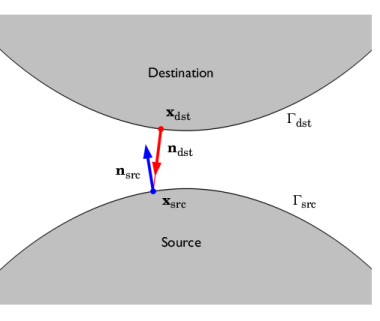
For each point xdst in the spatial frame on the destination boundary
Γdst, the closest point
xsrc in the spatial frame on the source boundary
Γsrc in the direction of the destination spatial normal
ndst is sought. Such a mapping can be described through and operator
map(E, x), where
E is some generic quantity or expression, and
x is the point to which
E is mapped. Using this mapping operator, the coordinates of the mapped point on
Γsrc is
where x is the spatial coordinates that parameterize
Γsrc. For brevity, the second argument of the mapping operator is omitted in the following and it should be understood that the mapping occurs to a point
xdst on
Γdst if nothing else is specified.
An important quantity for contact mechanics is the gap function ggeom(
x) defined as the geometric distance between the source and the destination boundary. Note that
ggeom(
x) is not necessarily the closest distance between the two boundaries. Using the mapping operator, the gap distance at
xdst is defined as
|
|
|
•
|
A Contact Pair sets up mapping operators that can be used in any expression to map quantities from the source to the destination boundary with the syntax src2dst_<pair_tag>(expr).
|
|
•
|
The mapping by default uses the spatial frame normal. If the Mapping method in the Contact Pair is changed to Initial configuration, the mapping is instead performed in the direction of the material frame normal. This means that the direction of the mapping is constant and not affected by how the contacting boundaries deform.
|
|
(3-161)
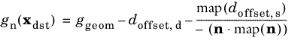
where doffset,s and
doffset,d is the offset from the source and destination boundary, respectively. Each offset variable can vary along the geometry, and may also vary in time (or by the parameter value when using the continuation solver). The correction of the source side offset is necessary since the normal of
xsrc,
nsrc=
map(
n), is not necessarily pointing towards
xdst as illustrated in
Figure 3-34. When the geometric surfaces are in contact, the normals will be exactly opposite.
(3-162)
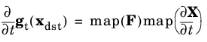
where X is the material coordinates, and
F is the deformation gradient that contains information about the local rotation and stretch. Both quantities are mapped from the source to the destination boundary. Constitutive models for the mechanical problem are typically formulated on an incremental form. COMSOL Multiphysics applies a backward Euler approximation to
Equation 3-162 so that the incremental slip at
xdst is
where Xsrc,old is the mapped material coordinates at the previous increment.
|
|
When a Contact node is added to the Shell, Layered Shell, or Membrane interfaces, the thickness of the structural element is included in the gap computation by considering the physical position of its top and bottom surface relative to the geometric boundary. The appropriate offset is then added to doffset,s and doffset,d. Similar corrections are also made when computing the incremental slip Δgt.
|
(3-163)
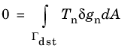
where Tn is the contact pressure, assumed positive in compression. To complete the contact condition,
Equation 3-163 is subjected to the Kuhn–Tucker conditions
(3-164)

where the first inequality represents the nonpenetration condition. Equation 3-163 and
Equation 3-164 together represents a unilateral constraint that require special techniques to implement. Several different techniques for doing so are available in COMSOL Multiphysics, which can be divided into two main classes: the
penalty method and the
augmented Lagrangian method.
For the penalty method, the contact pressure in Equation 3-163 is represented using a penalization of the physical gap so that
(3-165)
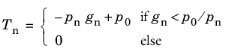
where pn is the penalty factor, and
p0 is the pressure at zero gap. This leads to an approximative solution of the non-penetration condition. The penalty method as defined by
Equation 3-165 is conceptually based on the insertion of a nonlinear spring between the contacting points. The penalty factor can be interpreted as the stiffness of that spring. A high value of the stiffness enforces the contact conditions more strictly, but if it is too high, it makes the problem ill-conditioned and unstable.
The pressure at zero gap, p0, can be used to reduce the overclosure between the contacting boundaries if an estimate to the contact pressure is known. In the default case, when
p0 = 0, there must always be some overclosure in order for a contact pressure to develop.
In addition to Equation 3-165, COMSOL Multiphysics also provides an alternative penalization based on a viscous formulation intended for transient simulations, referred to as the
Penalty, dynamic method. This formulation is based on the additional persistency condition
(3-166)
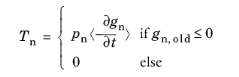
where gn,old is the physical gap distance at the previous increment, and <> is the positive parts operator. With the definition in
Equation 3-166,
Tn is only non-zero if the physical gap is negative during the entire increment, which is important for energy conservation during the initial contact event. However, there will always be some initial penetration before the gap rate is penalized. Hence the observed overclosure will be dependent on the size of the increment when two points come into contact. Note that this definition of the contact pressure implies that pressure contact is dissipative.
It is possible to use the definitions of Tn in
Equation 3-165 and
Equation 3-166 simultaneously. In such a case, they are additive and conceptually represent a parallel coupling of a spring and a dashpot.
(3-167)
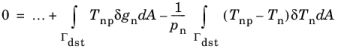
where Tnp is the penalized (or augmented) contact pressure, and
Tn is a Lagrange multiplier that can be identified as a contact pressure. The Lagrange multiplier representation of the contact pressure is defined as the dependent variable of the contact problem and is typically discretized using Lagrange shape functions. There are two methods for solving the above coupled system of equations, and this choice affects the definition of
Tnp.
The first solution method is referred to as a Segregated method and corresponds to the so-called Uzawa algorithm. Here, the system of equations is decoupled, and the displacement field
u and the Lagrange multiplier
Tn are solved in a segregated way. This leads to two levels of iterations in the solver, where
Tn is held constant when solving for
u, and vice versa when updating
Tn. For this solution method, the penalized contact pressure
Tnp is defined with a smooth transition to stabilize the problem when transitioning between contact states. The definition for
Tnp for outer iteration
j+1 is defined by
|
1
|
Initialize increment n+1 by setting the outer iteration counter j=0, and the initial values for dependent variables 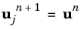 and 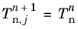
|
The appropriate solver sequence is automatically set up by COMSOL Multiphysics for the Segregated solution method when adding a new solver, or resetting to the default solver.
The alternative is to use a Fully Coupled solution method, which, as the name implies, amounts to solving the coupled system in
Equation 3-167 for the two dependent variables
u and
Tn (and any other variables included in the multiphysics model). When using this method, the penalized contact pressure is defined by
The Fully Coupled method can be convenient as it enforces the non-penetration condition exactly over the contacting boundaries, while it puts no restriction on how to set up the solver sequence. This flexibility can be especially advantageous when working with multiphysics problems, compared to the segregated approach. However, one should be aware that the method comes with some of the drawbacks of a pure Lagrange multiplier approach, albeit to a lesser extent. One drawback is that the solution typically is a saddle point, and convergence can be sensitive to how Newton iterations are made when solving the nonlinear problem.
In the limit, the Segregated and the
Fully Coupled solution methods converge to the same solution, but they can have different convergence properties.
In addition to the standard augmented Lagrangian method outlined above, an Augmented Lagrangian, dynamic method is available for transient simulations. As discussed for the penalty method, this formulation is based on the addition of the persistency condition. A segregated solution method is recommended for this method, and the main difference compared to the standard method lies in the definition of the penalized contact pressure. Both the non-penetration and persistency conditions are enforced by penalizing the rate of the physical gap distance so that
(3-168)
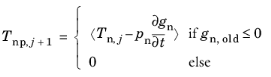
where gn,old is the physical gap distance at the previous increment, and <> is the positive parts operator. The same segregated solution strategy as described above is applied also when the dynamic method is used.
The Penalty, dynamic and
Augmented Lagrange, dynamic methods are based on a viscous type formulation, and dissipate energy when the contact is active. The accumulated dissipated energy
Wcntv can be computed by solving a distributed ODE on the destination boundary:
(3-169)

where Tt is the friction force. The stick and slip conditions are then enforced by the constitutive model used to define
Tt.
(3-170)
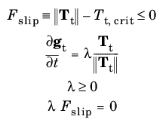
where Fslip is the slip function (analogue to the yield function in plasticity theory), and
λ is friction multiplier. The critical friction force
Tt,crit determines when slip occurs, and is defined as
where Tcohe is the cohesion, and
Tt,max defines the maximum friction force that is admissible. The friction coefficient
μ can either be defined as an arbitrary constant expression or through an exponential decay model in time-dependent studies. The latter model is defined as
where μstat is the static friction coefficient,
μdyn is the dynamic friction coefficient,
vs is the slip velocity, and
αdcf is a decay coefficient.
It is possible to also define the critical friction force through an arbitrary expression. In principle, Tt,crit, or any variable described above, may be defined as a function of any other variable or field. However, the implementation described in the following is only valid as long as it does not dependent on
Tt. In other words, the implementation of the friction constitutive model does not allow for hardening behavior of the friction force.
In COMSOL Multiphysics, implementation of Equation 3-170 is made using a backward Euler integration. Together with a penalty regularization, this results in the following set of algebraic equations to solve at increment
n+1:
where Tt,n is the friction force at the previous increment. The set of algebraic equations is solved for unknowns
Tt,n+1 and
λ by introducing a trial state and a return mapping. In doing so, it is assumed that
Tt,crit, n+1 is independent of
Tt, n+1, which leads to an explicit set of equations for finding
Tt, n+1. The trial state is first computed as
(3-171)
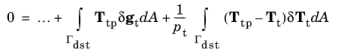
where Ttp is the penalized (or augmented) friction, and
Tt is a Lagrange multiplier that can be identified as a traction. The Lagrange multiplier representation of the tangential traction is defined as the dependent variable of the contact problem and is typically discretized using Lagrange shape functions. There are two methods for solving the above coupled system of equations,
Segregated and
Fully coupled, as selected in the parent
Contact node.
As for the penalty method, Equation 3-170 is implemented using backward Euler integration of the evolution equations, and a trial state and return mapping to solve the nonlinear algebraic equations.
When the Segregated solution method is selected in the parent
Contact node, the trial state for outer iteration
j+1 is computed as
This scheme then fits in to the algorithmic format described for normal contact where the displacement field u and the Lagrange multipliers associated with contact are solved in a segregated way. Including friction, this algorithm is schematically described as
|
1
|
Initialize increment n+1 by setting the outer iteration counter j=0, and the initial values for dependent variables 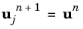 , 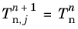 , and 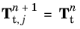
|
When the Fully coupled solution method is selected in the parent
Contact node, the trial friction force for iteration
i+1 is computed as
In the Slip Velocity subnode to
Contact, it is assumed the tangential contact is in a slip state when in contact, and that the relative motion between the source and destination boundaries is known beforehand. That is
where vslip is the prescribed velocity on the destination boundary relative to the source boundary. Given that the rate of the slip is known, the constitutive model for friction in
Equation 3-170 is simplified, and it follows that
Friction is a dissipative process and the accumulated dissipated energy Wfric can be computed by solving a distributed ODE on the destination boundary:
You can model a situation where two boundaries stick together once they get into contact by adding an Adhesion subnode to
Contact. Adhesion can only be modeled when the penalty contact method is used. The adhesion formulation can be viewed as if a thin elastic layer is placed between the source and destination boundaries when adhesion is activated.
Using the effective gap distance gn and the slip
Δgt, the adhesion formulation defines an incremental displacement jump vector
u in the local boundary system as
where Tb-T contains the transform from the global system to the boundary system. In the above expression, the Macaulay brackets indicate the positive parts operator such that
where k is the adhesive stiffness. For negative values of
gn, the normal component of
f is zero, and the contact condition is resolved by the penalty contact formulation. Notice that a different sign convention is used for the normal stress in the adhesion and contact contributions, where
Tn is positive in compression.
The adhesive stiffness k can be defined using three different options:
From contact penalty factor,
User defined, and
Use material data. For the first option, the normal stiffness is set equal to the contact pressure penalty factor
pn. The two tangential stiffness components are then assumed to be related to the normal stiffness, so that the stiffness vector equals
where nτ is a coefficient with the default value
0.17. This coefficient can either be input explicitly, or be computed from a Poisson’s ratio. A plane strain assumption is used for this conversion, giving
For the Use material data option,
k is calculated from the elastic constants of a fictive layer with a thickness equal to
ds.
When adhesion is active, it is possible to break the bond between the source and destination boundaries by adding a Decohesion subnode to
Contact. Decohesion modifies the stress vector
f defined by
Adhesion, but does not explicitly add any new contribution to the to the virtual work on the destination boundary. It thus requires an active
Adhesion node.
(3-172)
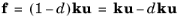
where d is the damage variable. During crack opening (or shearing), the damage variable grows, resulting in a softening behavior of the interface until it eventually breaks when
d = 1, see
Figure 3-36. If the interface is unloaded, the material follows the linear secant stiffness as defined by the current state of damage. No permanent deformations remain at complete unloading.
The Decohesion subnode implements the second term on the right-hand side of Equation 3-172, while the first term is implemented in
Adhesion. Notice that in the normal direction, damage only applies to separation of the boundaries, hence the normal contact is unaffected by decohesion.
In the displacement-based damage models, the damage variable d is defined using a damage evolution function written in terms of a displacement quantity. Since, in general, the fracture is a combination of mode I and mode II fracture, the model introduces a mixed mode displacement
um as the norm of the displacement jump vector.
where 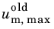 is and internal degree of freedom that takes the value of um,max
is and internal degree of freedom that takes the value of um,max at the previous converged solution. The damage variable is then defined as a function of
um,max of the form
where F-1 is called the damage evolution function and
u0m defines the onset of damage. Conceptually, the damage evolution function is the inverse of the softening branch of the traction separation law
F. Four different definitions of
F-1 are available in the
Traction separation law list. These damage evolution functions are summarized in
Figure 3-35, and the resulting traction separations laws in
Figure 3-36.
The Linear option specifies a damage evolution function that gives a bilinear traction separation law as seen in
Figure 3-36. It is defined as
where u0m and
ufm define the mixed mode initiation of damage and point of complete fracture, respectively. For the initiation of damage, a linear mixed mode criterion gives
(3-173)
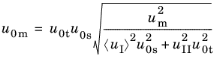
where uI and
uII are the mode I and mode II displacements, respectively. These are obtained from the displacement jump vector
u. The constants
u0t and
u0s are calculated as
(3-174)
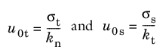
where σt is the tensile strength and
σs is the shear strength of the adhesive layer. The normal stiffness
kn and the equivalent tangential stiffness
kt are obtained from the adhesive stiffness vector
k. The mixed mode failure displacement
ufm depends on the selected
Mixed mode criterion. The
Power Law criterion is defined as
and the Benzeggagh-Kenane criterion is defined as
where Gct,
Gcs and
Gcm are the tensile, shear, and total energy release rates, respectively. The exponent
α is called the mode mixity exponent. From these relations, the mixed mode failure displacement can be calculated. For the power law criterion, the expression is
(3-175)

(3-176)
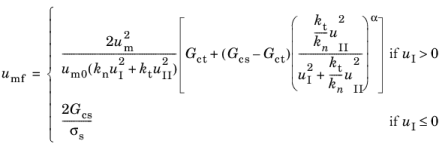
The Exponential option specifies a damage evolution function that gives a traction separation law which is linear up to the interface strength, and thereafter softens with an exponential curve that reaches zero asymptotically as seen in
Figure 3-36.
The mixed mode damage initiation displacement u0m is defined by
Equation 3-173 and
Equation 3-174. The mixed mode failure displacement
ufm is for the power law again given by
The Polynomial option specifies a damage evolution function that gives a traction separation law that is linear up to the interface strength. and thereafter softens with a cubic polynomial curve as seen in
Figure 3-36.
The Multilinear option specifies a damage evolution function that gives a traction separation law that is linear up to the interface strength. Thereafter a region of constant stress is introduced before the interface softens linearly as seen in
Figure 3-36.
The mixed mode damage initiation displacement u0m is defined by
Equation 3-173 and
Equation 3-174. The new constant
upm defines the end of the region of constant stress and requires the introduction of the shape factor
λ. The shape factor defines the ratio between the constant stress part of
Gct and the total “inelastic” part of
Gct:
Note that the shape factor is similarly defined for shear and is assumed to be equal for both components. Setting λ = 0 corresponds to the linear separation law. Using the above expression, the stress plateau displacement
upi for the respective component can be expressed as
where index i indicates either tension or shear. For the multilinear option, the mixed mode criterion is always linear (
α = 1). Hence the mixed mode stress plateau displacement and failure displacements are given as
From ψ(
u,
d), the stress vector
f and damage energy release rate
Ydm are obtained as
where 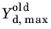 is and internal degree of freedom that takes the value of Ydm,max
is and internal degree of freedom that takes the value of Ydm,max at the previous converged solution. The energy dissipated during the decohesion process is
where Gcm is the critical energy release rate in the sense of fracture mechanics. The overall behavior of the cohesive zone model is then summarized by
where Yd0m defines the damage threshold and
F is a monotonically increasing function of the damage variable. From the above, an expression for the damage variable is obtained as
Three different definitions of F-1 are available under the
Traction separation law list for the energy-based damage model. These damage evolution functions are summarized in
Figure 3-37, and the resulting traction separations laws in
Figure 3-38.
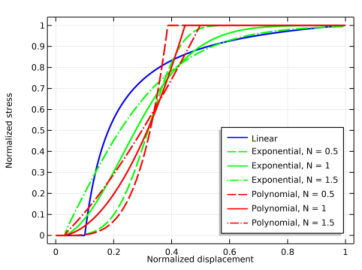
The Linear option specifies a damage evolution function that gives a bilinear traction separation law as seen in
Figure 3-38.
For the linear law, the equation constant Ydfm =
Gcm. The
Exponential option specifies a more general damage evolution function of the following form
where N is a smoothening parameter with a default value equal to 1. The effect of
N on the traction separation curve can be seen in
Figure 3-38. For the exponential law,
Ydfm is defined as
where Γ() is the gamma function. A similar damage evolution function is obtained by the
Polynomial option. It gives a generalized version of the traction separation law proposed in
Ref. 5 of the form
Left to determine are the two variables Yd0m and
Gcm. Their definitions require the introduction of a few new concepts related to the mixed mode loading. First, a mixed mode ratio is introduced
where uI and
uII are the mode I and mode II displacements, respectively. These are obtained from the displacement jump vector
u. The energy release rates of the respective modes are then given by
where G0t and
G0s define the damage threshold in tension and shear, respectively. The corresponding criterion for the fracture toughness is
where Gct and
Gcs are the critical energy release rates for tension and shear, respectively. The variables
α0 and
αc are called mode mixity exponents. Using these mode mixture rules results in
(3-177)

where d is the damage variable obtained from any of the available CZM, and
τ is the characteristic time that defines the delay of the decohesion. If the viscous damage is used to stabilize a rate-independent decohesion problem, the value of
τ must be chosen with care. As a rule of thumb,
τ should at least be one or two orders of magnitude smaller than the expected time step. Too large values of
τ can introduce significant amounts of extra fracture energy to the model, and the actual energy dissipated due to damage can exceed the defined critical energy release rates by orders of magnitude.
where Δt is the current time step taken by the time-dependent solver. The value of the viscous damage at the previously converged step

is stored as an internal degree of freedom.
By adding a Wear subnode to a
Contact node, it is possible to model adhesive or abrasive wear of the material when the contacting boundaries are sliding along each other. Since wear involves solving evolution equations, the
Wear node only adds a contribution for time-dependent studies.
The removal of material during the wear process can be modeled with two fundamentally different techniques. The most general technique is to model the removal using the deformed geometry concept. With this approach, the material frame X of the domains adjacent to the contacting boundaries is updated according to the computed wear depth
hwear. This means that there is an actual removal of material during the simulation which affects, for example, the contact search, mapping and conditions. When selecting the
Deformed geometry formulation, the wear feature adds a (hidden)
Deforming Domain feature that controls the material frame through an adaptive mesh smoothing. The removal of material is made through a (hidden)
Prescribed Normal Mesh Displacement boundary condition controlled by
hwear on the selected contact boundaries. By adding the deformed geometry, an extra dependent variable is added, the material mesh displacement
material.disp. This adds a set of extra degrees of freedom to the model that needs to be solved for.
Alternatively, the removal of material can be modeled using an offset-based approach. This formulation offers a simplified approach that is computationally less expensive, but mainly suitable when the amount of worn-off material is small. When selecting the Offset-based formulation,
hwear is subtracted from the offset variables
doffset,s and
doffset,d in
Equation 3-161. Hence, the material is considered removed only in the definition of the physical gap, while the contact search and mapping are unaffected. The latter follows from the fact that the actual coordinates and normals of the contacting boundaries essentially remain constant with respect to the wear; they, however, can change due to the deformation induced by the wear and changing contact conditions.
where the rate of the wear depth is given by some source term f that is typically a function of the slip velocity
vslip, the contact pressure
Tn, and the temperature
T. The surface and material properties also play an important role, and are represented by the generic quantity
θ in the above equation.
(3-178)
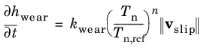
Here kwear is a dimensionless wear constant and the exponent
n controls the dependence of the wear rate on the contact pressure. The reference contact pressure,
Tn,ref, can be chosen arbitrarily, and is used only to obtain consistent units. The classical Archard wear equation is retrieved from
Equation 3-178 by setting
n =
1 and Tn,ref =
1 Pa. In addition, it is also possible to enter an arbitrary expression for the source term
f that defines the wear rate.
It is possible to account for wear on both the source and destination boundaries. However, it is generally more accurate to model wear on the destination side. This follows from the fact that most relevant quantities, such as Tn and
vslip, are defined only on the destination boundary in the
Contact node and by, for example, the
Friction node. Hence, when modeling wear on the source boundary, these quantities are mapped from the destination to the source. For example, when applied to the source side,
Equation 3-178 actually reads
