Wave Attenuation

For linear elastic isotropic material, the effective bulk and shear viscosity coefficients can be computed based on the spatial attenuation for elastic pressure and shear waves.

Without loss of generality, consider waves propagating along the x-axis. The waves are linear, so that small strains are assumed.

The pressure waves are solutions of the form:

. The corresponding momentum balance equation is

where the stress component can be represented as

where K and G are the bulk and shear moduli, respectively; ηb and ηv are the bulk and shear viscosity coefficients, respectively.

The shear waves are solutions of the form: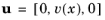

, where the y-polarization is assumed, again without loss of generality. The corresponding momentum balance equation is

where

Consider the following generic form of the momentum balance as a representation of either case, pressure or shear waves:

In an infinite domain, the solution can be expressed for any specified angular frequency ω in the following complex-values form:

where U+ and U- are constant amplitudes, and

are two solutions of the dispersion relation

Separation of the real and imaginary parts of the above equation gives

Note that for most materials,

even for very large values of ω.

The phase velocity is given by

The solution takes the form

which can be seen as a superposition of two plane waves propagating in the opposite directions; both waves are spatially attenuated in the corresponding direction of propagation.

For each wave, the spatial attenuation is characterized by α(ω) which is often called the attenuation coefficient. It has a SI unit (1/m), but is often given using neper per meter (Np/m). Alternatively, the value can be given in decibel per meter (dB/m). Both Np and dB are relative units (dimensionless). Values given in Np or Np/m can be used directly in any formula using SI units. The conversion formula needs to be applied for values using dB:

(value in Np) = (value in dB) ln(10)/20 = 0.1151 (value in dB)

The wave attenuation can be also specified as attenuation per wavelength λ, which is defined as

which allows to find the viscosity as

The the above formula can be directly applied to the cases of pressure and shear waves. Using given values of the attenuation per wavelength γp and γs measured in Np at the corresponding references frequencies fp,ref and fs,ref, the shear and bulk viscosity are found as

where

and

. If the values are given in dB per wavelength, the conversion factor ln(10)/20 needs to be inserted.

For given values of attenuation coefficients αp and αs measured in Np/m at the corresponding references frequencies fp,ref and fs,ref the approximate formulas for the viscosity coefficients are

where the approximate phase velocity for the pressure and shear waves are given by

and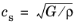

. If the values of αp and αs are given in dB/m, the conversion factor ln(10)/20 needs to be inserted.

Newnham R.E., Properties of Materials. Anisotropy, Symmetry, Structure. Oxford University Press, New York, 2005.

Ono K., “Review on Structural Health Evaluation with Acoustic Emission,” Applied Sciences, vol. 8, issue 6, p. 958, 2018; doi.org/10.3390/app8060958