Eigenfrequency Studies
The eigenfrequency equations are derived by assuming a harmonic displacement field, similar as for the frequency response formulation. The difference is that this study type uses a new variable jω explicitly expressed in the eigenvalue jω = −λ. The eigenfrequency f is then derived from jω as
Damped eigenfrequencies can also be studied, so λ is not necessarily a purely imaginary number. Any damping included in the problem will automatically cause the eigenfrequencies to become complex valued.
In addition to the eigenfrequency, the quality factor, Q, and decay factor, δ, for the model can be examined:
Modal Participation Factors
It is common to present modal participation factors in terms of the discretized system of equations, that is on matrix form. For a discretized system, the modal mass for the i-th mode can be defined as:
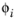
where Mnm is the mass matrix, and is the eigenmode in terms of a vector of degrees of freedom. The modal participation factors are defined as
where represent the unit rigid-body modes for translation and rotation.
The effective mass in direction j for mode i can then be computed as
For physics interfaces with only displacements as dependent variables (for example Solid Mechanics), each eigenmode is given by the solution vector . The rigid body modes ψ can be represented as columns of the following matrix:
where L represents a unit length.
The translational and rotational participation factors can be computed as, respectively:
and
where the normalization factor is computed as
The integration involves the entire selection of the corresponding physics interface. The definition of dm in the above formulas depends on the dimensions. For example, one has dm = ρdV for solid domains in 3D. Contributions to the structural mass come not only from the mass density of the domains, but also from features like Rigid Connector, Added Mass, Point Mass etc. Thus, integrations are in general performed over all selected domains, boundaries, and edges. Contributions from points are also added.
If the mass matrix normalization was selected when computing the eigenmodes, then mF = 1.
Note that the rotational participation factor computed with respect to a certain reference point r0 can be expressed in terms of the participation factors computed with respect to the origin as:
For structural elements (and features) that also use rotational degrees of freedom as dependent variables, there is also a direct contribution from these degrees of freedom. In this case, the corresponding expressions are:
with
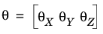
where matrix J presents the moment of inertia, and are rotation angles with respect to the corresponding axes. The angles can be computed at given local position as certain functions of the actual rotational degrees of freedom which can be different for different structural element types.
An alternative definition of the participation factors is:
where M denotes a unit mass. The advantage of such definition is independence of the normalization type selected when computing the eigenmodes.
The effective modal mass for X-translation and rotation are defined, respectively, as
and
Similar definitions are used for other components.
Only structural mechanics physics interfaces contribute to the mass and participation factor variables as described in this section. In a multiphysics context, there can be also other contributions to the total mass matrix. This would for example be the case when coupling acoustics and structural mechanics. Such contributions are not taken into account.