You are viewing the documentation for an older COMSOL version. The latest version is
available here.
A hyperelastic material is defined by its elastic strain energy density Ws, which is a function of the elastic strain state. It is often referred to as the
energy density. The hyperelastic formulation normally gives a nonlinear relation between stress and strain, as opposed to Hooke’s law in linear elasticity.
Most of the time, the right Cauchy–Green deformation tensor C is used to describe the current state of strain (although one could use the left Cauchy–Green tensor
B, the deformation gradient tensor
F, and so forth), so the strain energy density is written as
Ws(
C).
In the general case, the expression for the energy Ws is symbolically evaluated down to the components of
C using the invariants definitions prior to the calculations of the components of the second Piola–Kirchhoff stress tensor. The differentiation is performed in components on the local coordinate system.
|
|
In Equation View, the definitions of the stress components are shown as solid.Sl11 = 2*d(solid.Ws,solid.Cl11), solid.Sl12 = d(solid.Ws,solid.Cl12) etc. The factor 2 in front of the differentiation operator for the shear stresses is omitted, since the symmetry in the Cauchy–Green tensor will cause two equal contributions.
|
Here, the thermal volume ratio, Jth, depends on the thermal stretch
λth, which for linear thermal expansion in isotropic materials can be written in terms of the isotropic coefficient of thermal expansion,
αiso, and the absolute change in temperature
Here, the term αiso(T−Tref) is the
thermal strain. The isotropic thermal gradient is therefore a diagonal tensor defined as
When the coefficient of thermal expansion α is anisotropic, the thermal strain is computed from
where βh is the coefficient of hygroscopic swelling,
cmo is the moisture concentration, and
cmo,ref is the strain-free reference concentration. The coefficient of hygroscopic swelling can represent isotropic or anisotropic swelling. The anisotropic hygroscopic gradient is defined as
Here, the plastic deformation tensor Fpl depends on the plastic flow rule, yield function, and plastic potential.
For some classes of hyperelastic materials it is convenient to split the strain energy density into volumetric (also called
dilatational) and
isochoric (also called
distortional or
volume-preserving) contributions. The elastic deformation tensor is then multiplicatively decomposed into the volumetric and isochoric components
with Fel,vol as the volumetric elastic deformation (a diagonal tensor) and
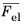
the isochoric elastic deformation gradient. Isochoric deformation means that the volume ratio is kept constant during deformation, so the isochoric elastic deformation is computed by scaling it by the elastic volume ratio. The elastic volume ratio is defined by
By using Jel it is possible to define the
isochoric-elastic deformation gradient
the isochoric-elastic right Cauchy–Green tensor
and the isochoric-elastic Green–Lagrange strain tensor
Some authors call 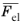 and
and 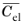 the modified
the modified tensors. Note that
The other two invariants normally used together with Jel are the first and second invariant of the isochoric-elastic right Cauchy–Green deformation tensor
If the Nearly incompressible material is selected in the
Compressibility list in the
Hyperelastic Material node, the total strain energy density
Ws is split into two parts:
here, Wiso is the isochoric strain energy density and
Wvol is the volumetric strain energy density.
The volumetric strain energy density, Wvol, is defined as an expression of the elastic volumetric deformation
Jel. The
quadratic volumetric strain energy density is defined as:
(3-36)
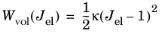
and Hartmann–Neff volumetric strain energy density (
Ref. 10) as:
(3-37)
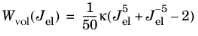
where κ is the bulk modulus. The default value for the bulk modulus is 100 times the initial shear modulus for the given hyperelastic material model. From here, the volumetric stress (pressure) is calculated as
When the expression in Equation 3-36 is used, the pressure becomes linearly related to the volume change:
but if the expression in Equation 3-37 is used instead of the quadratic function, the pressure becomes a nonlinear function of the volume change:
Then, an auxiliary variable, pw, is added to map the pressure when computing stresses.
(3-38)
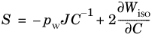
When the Incompressible material is selected in the
Compressibility list in the
Hyperelastic Material node, the volumetric strain energy density
Wvol is not defined as for
Nearly Incompressible Hyperelastic Materials, but instead, a weak constraint is added to account for the incompressibility condition
The auxiliary variable, pw, acts as Lagrange multiplier to enforce the constraint
Jel = 1, this variable is then used as the pressure when computing stresses.
The strain energy density Ws consists only of the isochoric strain energy density
Wiso contribution
(3-39)
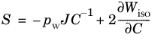
(3-40)
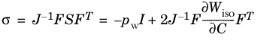
A numerical scheme is said to exhibit locking if the accuracy of the approximation deteriorates as a parameter tends to a limiting value (
Ref. 12). Finite elements in solid mechanics are said to “lock” when exhibiting an unphysical response to deformation (
Ref. 13). Locking can occur for many different reasons. For linear elastic materials, this typically happens as Poisson’s ratio tends to 0.5, or the bulk modulus is much larger than the shear modulus. Numerical errors arise because the shape functions are unable to properly describe the volume preserving deformation.
To avoid the locking problem in computations, the mixed formulation replaces pm in
Equation 3-38 with a corresponding interpolated pressure help variable
pw, which adds an extra degree of freedom to the ones defined by the displacement vector
u.
Here, λ and
μ are the Lamé parameters (SI unit: Pa).
and the elastic volume ratio Jel and the bulk modulus
κ to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Here, λ and
μ are Lamé parameters (SI unit: Pa). The bulk modulus
κ is calculated from the Lamé parameters
κ = λ + 2μ/3.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials.
The material parameters C10 and
C01 (SI unit: Pa) are related to the Lamé parameter (shear modulus)
μ = 2(C10 + C01). The elastic volume ratio
Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Rivlin and Saunders (Ref. 2) proposed a phenomenological model for small deformations in rubber-based materials on a polynomial expansion of the first two invariants of the elastic right Cauchy–Green deformation, so the strain energy density is written as an infinite series
with C00 = 0. This material model is sometimes also called
polynomial hyperelastic material.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
where  and
and 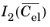 are the isochoric invariants of the elastic right Cauchy–Green deformation tensors. The elastic volume ratio Jel
are the isochoric invariants of the elastic right Cauchy–Green deformation tensors. The elastic volume ratio Jel and the bulk modulus
κ to are used to define the volumetric strain energy density, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Yeoh proposed (Ref. 1) a phenomenological model in order to fit experimental data of filled rubbers, where Mooney–Rivlin and Neo-Hookean models were to simple to describe the stiffening effect in the large strain regime. The strain energy was fitted to experimental data by means of three parameters (SI unit: Pa), and the first invariant of the elastic right Cauchy–Green deformation tensors
I1(Cel)
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Here μp (SI unit: Pa) and
αp (dimensionless) are material parameters, and
λel1,
λel2, and
λel3 are the principal elastic stretches such as
Jel = λel1λel2λel3.
The Ogden model is empirical, in the sense that it does not relate the material parameters αp and
μp to physical phenomena. The parameters
αp and
μp are obtained by curve-fitting measured data, which can be difficult for
N > 2. The most common implementation of Ogden material is with
N = 2, so four parameters are needed.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
The Storakers material (Ref. 13 and
Ref. 19) is used to model highly compressible foams. The strain energy density is written in a similar fashion as in Ogden material:
for constant parameters
βk = β, the initial bulk modulus becomes
κ = 2μ(β + 1/3), so a stable material requires
μ > 0 and
β > −1/3. In this case, the Poisson's ratio is given by
ν = β/(2β+2/3), which means that for a Poisson’s ratio larger than
−1, β > −2/9 is needed.
The Varga material model (Ref. 1) describes the strain energy in terms of the elastic stretches as
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Arruda and Boyce (Ref. 3) derived a material model based on Langevin statistics of polymer chains. The strain energy density is defined by
Here, μ0 is the initial macroscopic shear modulus,
I1(Cel) is the first invariant of the elastic right Cauchy–Green deformation tensor, and the coefficients
cp are obtained by series expansion of the inverse Langevin function.
Other authors (Ref. 1) use only the first three coefficients of the series. The number of segments in the polymeric chain is specified by the parameter
N so the material model is described by only two parameters,
μ0 (SI unit: Pa) and
N. This material model is sometimes also called the
eight-chain model.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Many hyperelastic material models are difficult to fit to experimental data. Gent material (Ref. 14 and
Ref. 15) is a simple phenomenological constitutive model based on only two parameters,
μ and
jm, which defines the strain energy density as:
Here, μ (SI unit: Pa) is the shear modulus and
jm (dimensionless) is a limiting value for
I1− 3, which takes care of the limiting polymeric chain extensibility of the material.
Since the strain energy density does not depend on the second invariant I2, Gent model is often classified as a generalized Neo-Hookean material. The strain energy density tends to be the one of incompressible Neo-Hookean material as
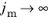
.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials. Gent material is the simplest model of the limiting chain extensibility family.
Here, μ (SI unit: Pa) is the shear modulus. The maximum chain stretch
λm (dimensionless) represents a limiting value for the averaged invariant
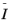
, which accounts for the maximum chain extensibility in networks with finite chain lengths. The dimensionless parameter
β phenomenologically averages the two isochoric invariants
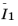
and
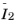
, and the parameter
α (dimensionless) represents the global interaction between polymer chains.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials
Here, φ is an interpolation parameter bounded to
0 < φ < 1, the parameter
μ (SI unit: Pa) is the shear modulus, and
β is an expression of Poisson’s ratio.
In the special case of φ = 1, the strain energy reduces to a similar form of the Neo-Hookean model
Gao proposed (Ref. 20) a simple hyperelastic material where the strain energy density is defined by two parameters,
a (SI unit: Pa) and
n, and two invariants of the elastic right Cauchy–Green deformation tensors
Cel:
Here, the invariant I-1(Cel) is calculated as:
Gao proposed that the material is unconditionally stable when the parameters are bounded to 1 < n < 3 and
0 < a, and related these parameters under small strain to the Young’s modulus and Poisson’s ratio by:
Since n = (1+ν)/(1−2ν) and it is bounded to
1 < n < 3, this material model is stable for materials with an initial Poisson’s ratio in the range of
0 < ν < 2/7.
Here, l,
m, and
n (SI unit: Pa) are the Murnaghan third-order elastic moduli, which can be found experimentally for many commonly encountered materials such as steel and aluminum, and
λ and
μ are the Lamé parameters.
Delfino proposed a simple hyperelastic material for modeling carotid arteries (Ref. 22). The strain energy density is defined by two parameters,
a (SI unit: Pa) and
b, and the first invariant of the isochoric elastic right Cauchy–Green deformation tensors

:
The parameter a plays the role of shear modulus at the small strain limit.
Fung (Ref. 22) proposed one of the most popular strain energy functions to describe the deformation in soft biological tissues and arteries. For this hyperelastic material, the strain energy density reads
the parameter c (SI unit: Pa) scales the global stiffness, and the quadratic form
Q (dimensionless) depends on the Green–Lagrange strain
here, A is a six by six symmetric matrix (dimensionless), and
E is a vector which contains the elements of the elastic Green–Lagrange strain tensor sorted in either standard or Voigt order, see
Orthotropic and Anisotropic Materials.
The elastic volume ratio Jel and the bulk modulus
κ are used to define the volumetric strain energy density
Wvol, see
Nearly Incompressible Hyperelastic Materials. The incompressible option uses the same isochoric strain energy as when selecting the nearly incompressible option, but an extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
The term Wc represents the energy from the cross-linking of the network, and
We represents the energy from confining tube constrains. These are written as
Here, Gc and
Ge are material parameters (SI unit: Pa),
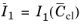
is the first invariant of the elastic right Cauchy–Green deformation tensor,
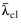
are the isochoric principal stretches, and
α and
β are dimensionless coefficients.
The parameters Gc and
Ge plays the role of shear modulus at the small strain limit,
G0 = Gc + Ge. The parameter
α corresponds to the maximum finite chain extensibility, as the strain energy
Wc is singular for stretch values such as
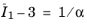
.
For Compressible hyperelastic materials, enter an expression for the elastic strain energy
Ws, which can include any expressions involving the following:
|
•
|
Components of Cel, the elastic right Cauchy–Green deformation tensor in the local material coordinate system.
|
|
•
|
Principal elastic stretches λel1, λel2, and λel3, which are the square-root of the eigenvalues of the elastic right Cauchy–Green deformation tensor Cel.
|
the invariants of εel are written in terms of the invariants of
Cel:
When the Nearly incompressible material option is selected for the
Hyperelastic Material node, the elastic strain energy is decoupled into the volumetric and isochoric components.:
|
•
|
The isochoric strain energy, Wiso, as an expression involving the invariants of the isochoric elastic right Cauchy–Green tensor 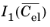 and 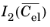 ; the invariants of the isochoric elastic Green–Lagrange strain 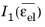 , 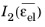 , and 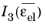 ; or the principal isochoric elastic stretches defined as 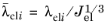
|
When the Incompressible material option is selected, enter an expression for the isochoric elastic strain energy
Wiso, as done for the
Nearly incompressible material option. An extra variable is added to enforce the incompressibility condition
Jel = 1, see
Incompressible Hyperelastic Materials.
Ogden and Roxburgh (Ref. 34) used an additional state variable to model the Mullins effect. The state variable
η is introduced to memorize the microstructural damage on reinforced rubber after repeated loading-unloading cycles. The modified isochoric strain energy density reads
here, Wiso is the isochoric strain energy of the undamaged material, and
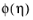
is referred as the
damage function. The choice of the damage function
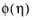
is completely arbitrary as long as some constrains are fulfilled. The authors (
Ref. 34) proposed a state function based on the
error function, which defined how the state variable
η varies as a function of the isochoric strain energy
here, erf(.) is the error function,
r and
m are positive parameters, and
Wmax is the maximum attained value of the isochoric strain energy density on the loading path.
Over the years others authors (Ref. 35-
36) have proposed different flavors of Ogden–Roxburgh model, the version implemented in COMSOL Multiphysics uses by default the
hyperbolic tangent function, and a parameter to define the maximum allowed damage
d∞=1/r. The microstructural damage is then computed from
Here, d∞,
α, and
Wsat are positive parameters. It is also possible to use the
error function as in the original formulation (
Ref. 34), in which case the microstructural damage is computed from
Miehe (Ref. 37) proposed an exponential expression for the damage variable in order to model the Mullins effect
where Wsat and
d∞ are positive parameters.