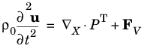The first Piola–Kirchhoff stress P is calculated from the second Piola–Kirchhoff stress as P = FS. The first Piola–Kirchhoff stress relates forces in the present configuration with areas in the reference configuration, and it is sometimes called the nominal stress.

where the density corresponds to the material density in the initial undeformed state, the volume force vector FV has components in the actual configuration but given with respect to the undeformed volume, and the tensor divergence operator is computed with respect to the coordinates on the material frame. Equation 3-14 is the strong form that corresponds to the weak form equations within the Solid Mechanics interface (and many related multiphysics interfaces) in COMSOL Multiphysics. Using vector and tensor components, the equation can be written as

The boundary load vector FA in case of geometric nonlinearity can be related to the first Piola–Kirchhoff stress tensor via the following formula:

where the normal n0 corresponds to the undeformed surface element. This force vector is often referred to as the nominal traction. In components, it can be written as

The Cauchy stress, σ, can be calculated as

The Cauchy stress is a true stress that relates forces in the present configuration (spatial frame) to areas in the present configuration, and it is a symmetric tensor. Equation 3-14 can be rewritten in terms of the Cauchy stress as

where the density corresponds to the density in the actual deformed state, the volume force vector fV has components in the actual configuration (spatial frame) given with respect to the deformed volume, and the divergence operator is computed with respect to the spatial coordinates.