Modeling Imperfection in a Buckling Analysis
Real structures always contain some level of imperfections in the geometry. Beams are not perfectly straight, plates are not perfectly flat, etc. For some structures, the real-life failure load is much smaller than the ideal buckling load that would be the result of a linearized buckling study.
There are different ways in which you can take imperfections into account. If the actual imperfections are known, they may even be part of the geometry. More common, however, is that the analysis is based on the ideal geometry. In this case, using the deformed geometry concept provides a convenient tool for introducing the imperfection.
For more information about deformed geometries, see Deformed Geometry and Moving Mesh and Deformed Geometry Features in the COMSOL Multiphysics Reference Manual
If the imperfection is known from some external source, say a standard that stating that a certain curvature must be assumed for a beam, then you can directly enter expressions for such deviations. Do as follows:
1
On the Definitions tab, click Deformed Geometry, and select Prescribed Deformation. Alternatively, you can right-click on the Component node and select Deformed Geometry>Prescribed Deformation.
2
In the added Prescribed Deformation node, select the appropriate Geometric entity level, and then select the part of the geometry to perturb.
3
Enter expressions for the Prescribed deformation in terms of the geometry frame coordinates, for example Xg, Yg, and, Zg.
Another common approach for generating an initial imperfection is to first perform a linearized buckling analysis, and then add one or more suitably scaled buckling modes as initial imperfection. The rationale behind this is that it is reasonable to assume that the structure is sensitive to an imperfection that resembles a buckling mode.
The procedure for entering buckling models as imperfections is also based on a deformed geometry, but is more complicated. For this reason, a special tool is available for setting up such an analysis, as described below.
1
Run a linear buckling analysis, in which you solve for one or more buckling modes.
2
On the Definitions tab, click Physics Utilities, and select Buckling Imperfection. Alternatively, you can right-click on the Definitions node and select Physics  Utilities>Buckling Imperfection.
3
In the added Buckling Imperfection node, do the following
a
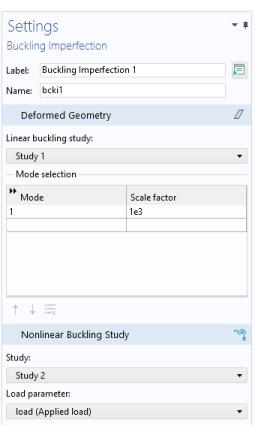
From the Linear buckling study list, choose the study from which the imperfection mode shapes are to be selected. Only studies containing a Linear Buckling study step are shown in the list.
b
Under Mode selection, add the buckling modes to include in the Mode column. Also, specify a scale factor for each mode in the corresponding field under Scale factor.
c
To add a Deformed Geometry node with necessary subnodes in which the selected sum of buckling modes are used as predeformation, click the Create button () in the Deformed Geometry section header.
d
From the Study list, choose the study that is the nonlinear buckling study. The default, and most common case, is New, in which case the study does not already exist. You can also select any existing Stationary study.
e
From the Load parameter list, choose the parameter to use as a load parameter for ramping up the load. The parameter must be defined under a Parameters node, so you may have to move there to create it. Its purpose is to act as a multiplier to the same load that was used in the linear buckling study.
f
Click the Create button () in the Nonlinear Buckling Study section header to set up the nonlinear study. If Study is set to New, a new study is created. If an existing study is selected, its settings will be modified. In either case, geometrical nonlinearity will be activated in the study, and a continuation solver will be set up using the Load parameter as auxiliary sweep parameter. The range of the sweep is based on the lowest buckling mode selected in the Mode selection table.
Figure 2-30: Settings in the Buckling Imperfection node.
4
Go back to the physics, and make sure that the loads are multiplied by the load multiplier parameter.
5
Run the nonlinear buckling study.
•
When the nonlinear study is generated, the default expression for the auxiliary sweep parameter values is set to
<CritFactor>*log(range(1,1,20))/log(15)
Here, <CritFactor> is the critical load factor in the linearized buckling analysis. This means that the load is increased in 20 decreasing steps, from 0 to about 1.1 times the critical load factor.
•
Under Definitions, a Deformed Geometry node with one or more Prescribed Deformation subnodes is created. These subnodes contain references to special variables containing the selected superposition of buckling modes (Figure 2-31).
Figure 2-31: The automatically generated deformed geometry settings.
Linear Buckling Analysis of a Truss Tower: Application Library path Structural_Mechanics_Module/Buckling_and_Wrinkling/truss_tower_buckling