Reduced-order modeling seeks to reduce the number of degrees of freedom in a physical model whilst still retaining the essential physics. For a lightly damped resonant system driven at one of its resonant frequencies, it is reasonable to consider only the contributions to the system of a small number (m) of modes within the signal bandwidth. In some cases, a single mode is sufficient. A system with n degrees of freedom has mass, stiffness, and damping matrices of size n-by-n. A reduced-order representation of the system considering m modes has size m-by-m. The reduction in complexity of the system, and the computational speed up is therefore significant when m « n. This section describes the theory of the reduced-order system and gives guidelines on how to obtain reduced-order models from a COMSOL model.

Consider a mechanical system, with n degrees of freedom, described by an equation of the form

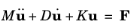
where u is the displacement vector (size: n-by-1), K is the stiffness matrix (size: n-by-n), D is the damping matrix (size: n-by-n), and M is the mass matrix (size: n-by-n). In the frequency domain the problem takes the form

where u = u0eiωt.

Initially consider the system in the absence of damping and forces. The undamped system has n eigenvalues ωi, which satisfy the equation

These eigenvectors can be shown to be orthogonal with respect to both M and K:

Next the following n-by-n matrix is constructed, with columns taken from the n eigenvectors:

From Equation 2-7 it is clear that this is a diagonal matrix. Similarly, from Equation 2-8 it is clear that UTKU is also diagonal.

From the properties of the eigenvectors it is possible to expand any function in terms of the eigenvectors. Thus, the displacement u can be written as:

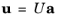
where a is a column vector containing the coefficients ai as rows. In general a is time-dependent.

Now consider the original equation: Equation 2-5. First substitute for u using Equation 2-9. Then transform the equation to the modal coordinate system by premultiplying by UT. This gives:

It has already been established that the matrices UTMU and UTKU are diagonal and frequently a damping model is chosen that results in a diagonal damping matrix. For example, in Rayleigh damping D = αM + βK, where α and β are constants. For a general damping, the transformed damping matrix is however not diagonal. As an alternative, a damping ratio, ζi, can be assigned to each mode.

The precise form of Equation 2-10 is determined by the normalization adopted for the eigenfunctions. In structural applications the eigenfunctions are often normalized such that UTMU = I. This is referred to as mass matrix scaling in the eigenvalue solver. In this case Equation 2-6 gives

where diag(ωi2) is the diagonal matrix with diagonal elements ωi2. Similarly, if damping ratios for each mode are defined, the damping matrix can be expressed in the form

Thus, if mass matrix scaling is used Equation 2-10 takes the form

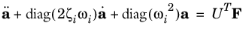
It is also possible to scale the eigenvectors so that the point of maximum displacement has given displacement. This is referred to as max scaling in the eigenvalue solver. For an individual mode this scaling has a simple physical interpretation — the corresponding component of a, ai, is the amplitude of the i:th mode, measured at the point of maximum displacement, when the mode is driven by the force F. In this case Equation 2-10 takes the form

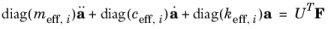
Here meff,i is the effective mass of the i:th mode, ceff,i = 2meff,iξiωi is the effective damping parameter for the mode, and keff,i is the effective spring constant. Each element of the vector UTF gives the force component that acts on each of the respective modes.

The preceding discussion did not consider how to reduce the number of degrees of freedom in the system. For systems in which the vector UTF has only a few significant components (for example, components i = 1, …, m where m « n) the following approximation can be made:

The expression for u in matrix becomes:

where U' is now an m-by-n and a' is a vector with m components. The equation system in modal coordinates now takes the form

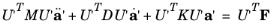
The matrices U'TMU', U'TDU', and U'TKU' now have dimensions m-by-m. Similarly, the vector U'TF has m components. This results in a significant reduction in the system complexity.

If physically relevant damping is present in the system, the above theory must be modified as the damping matrix is no longer diagonal in the modal coordinate system. COMSOL can still handle this case as the modal solver does not assume that any of the matrices are diagonal. In this case the eigenvalues become complex and the eigenvectors split into right and left eigenvectors. The right eigenvectors Ur are solutions of the equation:

where U'r is the n-by-m matrix containing the right eigenvectors chosen for the modal analysis. Once again a' is a vector with m components. The system in modal coordinates takes the form

where U'l is the n-by-m matrix containing the left eigenvectors chosen for the modal analysis.

The matrices U'lTMU'r, U'lTDU'r, and U'lTKU'r are no longer necessarily diagonal. The modal solver accepts any linearly independent set of vectors to project the solution vector and equations onto and constructs the reduced-order system accordingly.

The Model Reduction and Modal Reduced Order Model study steps have the property that they can assemble the modal matrices and make them available for output. In the Model Reduction node, the Store reduced matrices check box must be selected.

After the model has solved, right-click the Results>Derived Values node and select System Matrices. In the output section choose the Matrix to display in the list. The mass matrix corresponds to the matrix U'lTMU'r the stiffness matrix corresponds to U'lTKU'r, and the damping matrix corresponds to U'lTDU'r. The vector U'lTF is available as the load vector. These matrices are given in a format that respects the normalization of the preceding Eigenvalue Solver. To change this, select the Eigenvalue Solver node, and change the Scaling of Eigenvectors setting under the Output section. Use the Max setting if an equivalent Mass-Spring-Damper system is required, in which case the modal amplitude corresponds to the maximum displacement of the mode.