Cross-Section Properties

The following cross-section properties computed by the Beam Cross Section interface are described in this section:

The moments of inertia in the XY coordinate system are:

Since the input data required by the Beam interface is the principal moments of inertia, these must also be computed. Using the radius of the Mohr’s circle:

the principal moments of inertia can be expressed as:

As an auxiliary variable, the radius of gyration is computed, using the expression

The angle needed to rotate the x-axis to the axis of the largest principal moment of inertia (x1) is denoted α. From the definition of Mohr’s circle, the angle is:

When implemented using the atan2 function, the angle can be correctly evaluated for all rotations, and returns in the interval -π < α < π.

The local coordinate system, having its origin in the center of gravity, and orientation given by the principal moments of inertia is given by:

The shear stresses caused by bending cannot be given a simple closed form solution, but must be solved using two independent partial differential equations, one for the force in each direction. The complete derivation is given at the end of this section. First some quantities computed from the shear stresses are defined.

The following notation is used: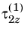

. This is a shear stress in the x2 direction (acting on the plane with z as normal) caused by a unit shear force acting in the x1 direction.

The max shear stress factor is the ratio between the maximum shear stress in the cross section and the average shear stress. For a shear force in the x1 direction, the definition is:

where

is the resulting shear stress from a unit load in the x1 direction. Similarly:

The shear correction factor is also computed. The shear correction factor is a multiplier which makes the strain energy from the average shear stress and shear strain in the cross section equal to the true shear energy in the cross section. The shear correction factor can be introduced through the concept shear area. The shear area is the reduced area which should replace the true area when computing the shear deformation of a beam. In terms of the shear correction factor it can be written as:

where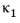

is the shear correction factor for a shear force in the x1 direction. Thus, for a shear flexible beam, the constitutive relation for the average shear is

To compute the shear correction factor, the true strain energy based on the actual stress and strain distribution is set equal to the strain energy from the average shear stress, when acting over the shear area. The full energy expression is

The strain energy based on the averaged shear stress and shear strain is

giving

Since T1 is a unit shear force, the shear correction factor can be computed as

Similarly:

The shear center (or, equivalently, the center of rotation) is the point around which the shear stresses from bending has no torque. In COMSOL it is represented as the distance from the center of gravity of the cross section in the principal axes coordinate system. The torque can be computed as:

Since there are two separate solutions for the shear stresses, it is possible to split the determination of the two shear center coordinates into:

Here the fact that the shear force resultant has a unit value has been used.

Basic beam theory assumptions give the following stress components:

The shear forces are related to the bending moments through

The static equilibrium equations are:

Insertion of the known stresses into the equilibrium equations gives:

The two first equations simply state that the shear stresses are independent of z, whereas the third equation is the one on which to focus the interest. Assume that the shear stresses can be derived from a scalar stress potential,

, through:

Insertion of this assumption into the third equilibrium equation gives the Poisson type equation:

In addition to equilibrium, also compatibility must be fulfilled. The Beltrami-Michell form of compatibility equations includes the assumption of an isotropic linear elastic material, and then states that:

Given the stress state from Equation 9-1, the only two nontrivial equations are:

Inserting the assumed stress components gives:

Integration of the first equation with respect to x1 and the second equation with respect to x2 gives:

Combining these two equations results in:

This is the same equation as Equation 9-2. It is thus possible to fulfill equilibrium, compatibility, and the constitutive relation with a single equation of Poisson type.

On all free boundaries, the stress must be zero, giving the condition:

Using the assumed shear stresses, this can be converted into the Neumann condition:

It must also be determined that the resultant of the shear stresses actually match the applied shear forces, that is:

The proofs for the two components are analogous, so it is shown only for the x1 direction:

To compute the integral of the x1 derivative of

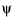
, a term containing the differential equation itself is added. This is a zero contribution, but it makes further simplifications possible.

In the transformations above these facts are used:

This proves that the assumed stress field also produces the correct resultants.

When internal holes are present, it is necessary ensure compatibility in the sense that the displacement is single valued when going around the hole:

The displacements can be derived from the strains, which are given by the stress state:

Integration of the direct strains gives:

Since the only part of the displacement that is relevant for the bending shear stresses is independent of the z coordinate, the functions g1 and g2 can be considered as independent of z.

In the last transformation Green’s theorem is used. The uniqueness of the u2 displacement can be shown in the same way.

The uniqueness of the out-of-plane component of the displacement is shown in Equation 9-3:

In the last step of Equation 9-3, all integrals are zero since the coordinate system is located at the center of gravity of the section. This proves that all displacement components are unique.

When solving the problem, the shear stresses caused by a unit force in each of the two principal directions must be separated, so two separate problems are solved. For the force in the x1 direction it is formulated as:

with

on all boundaries. The stresses are computed as:

The corresponding problem for the x2 direction is:

The torsional properties cannot in general be computed using a closed form expression. Determining the torsional rigidity requires the solution of a PDE over the cross section. There are two ways to do this: Using a warping function or using the Prandtl stress function. The Prandtl stress function approach is used in COMSOL since it gives easier boundary conditions.

The general torsion theory includes the shear modulus and angle of twist, but these properties are not needed to determine the torsional rigidity, so both parameters are treated as having the value 1. In that case the equation to be solved can be simplified to:

where φ is the stress function. For a singly connected region the boundary condition is

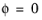
along the whole boundary. Having solved this problem, the torsional rigidity can be computed as:

The shear stresses are defined as:

The torsional modulus can be determined as:

In the case that there are internal holes in the section the situation is slightly more complex. The

condition is now applicable only to the external boundary, whereas each boundary of an internal hole i needs a Dirichlet boundary condition:

where

is a constant to be determined. The constant value of the stress function fulfills the stress-free boundary conditions. There is also a compatible condition that must be fulfilled: the displacements must be single valued when going around each hole along its boundary

. This is trivially fulfilled for the in-plane displacements, but the out-of-plane displacement, w, generates the necessary equations to determine

:

Here it has been used so that the strains are equal to the stresses since the shear modulus is set to 1. The kinematic assumption that the in-plane displacements can be written as:

is employed. This assumption implies that the origin of the coordinate system is at the center of rotation. This is true only for doubly symmetric sections, but adding a constant offset to the x and y coordinates does not contribute to the integral.

Since the gradient of φ depends linearly on the yet unknown variables

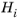
, the values of which can be solved by adding one equation:

for each hole.

The expression for the torsional rigidity must in this case be augmented to:

where

is the area of hole i.

The warping properties of the cross section are not used by the Beam interface in COMSOL Multiphysics, since an assumption of pure St Venant torsion is used. The data can still be useful to do manual estimates.

The warping function

describes the out-of-plane deformation related to torsion. It fulfills the Laplace equation

.

The boundary conditions giving stress-free boundaries:

The offset by the shear center coordinates (ex, ey) is introduced since the torsion theory assumes that the coordinate system has it origin in the center of rotation (which is the same as the shear center).

The level of the warping function must also be fixed by adding a Dirichlet condition in a point. The actual value is however difficult to set. Instead it is easier to solve for a shifted warping function: