Space charge regions develop at the interface between two different semiconductors, as a result of the change in the band structure that occurs at the junction. Such interfaces are referred to as heterostructures. COMSOL Multiphysics handles all interior boundaries in a model using the Continuity/Heterojunction feature, which automatically detects whether a change in the band structure occurs at the interface. For interior boundaries within a single material, the electron and hole densities are continuous and the boundary has no effect on the solution. When a heterostructure is present, one of the following Continuity model options should be selected from the Heterojunction settings:

where Efn1 and Efp1 are the electron and hole quasi-Fermi levels in material 1 and Efn2 and Efp2 are the electron and hole quasi-Fermi levels in material 2.

The thermionic emission boundary condition is based on Ref. 27.

where n1·Jn1 is the outward normal electron current from material 1, n2·Jn2 is the normal electron current leaving material 2, n1·Jp1 is the outward normal hole current from material 1, n2·Jp2 is the normal hole current leaving material 2. vn1, vn2, vp1, and vp2 are the electron and hole recombination velocities for each material at the boundary. n1, n2, p1, and p2 are the electron and hole concentrations on each side of the boundary. Other quantities are defined in Figure 3-16. The recombination velocities are given by:

where the effective Richardson’s coefficients An1*, An2*, Ap1*, and Ap2* are given by:

The effective masses in the above equations are assigned the smaller value of the density of states effective mass between the 2 domains according to Ref. 27. The effective mass can be altered in the equation view if required.

The effect of tunneling can be accounted for by including an extra proportional factor δ in the thermionic current density, using the formulas derived in Ref. 27 (based on the WKB approximation).

The electron and hole normal current densities given in Equation 3-143 are multiplied by a factor of (1+δnJn) and (1+δnJp), respectively. The extra current factors δnJn and δnJp are given by the double integration along the electrical field line (dl) and along the energy axis (dVx):

where h is the Planck constant, the limits of the energy axis integration are given by

where the max function of the second equation is taken within the domain selection of the potential barrier, and the potential barrier variable Eb is given by

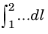
and Eb1 and Eb2 are the values of Eb at the two opposite boundaries 1 and 2 across the potential barrier and connected by an electric field line, evaluated on the side of each boundary that is (immediately) outside of the potential barrier domain selection. The integral is the line integral along the electric field line between the two opposite boundaries 1 and 2 across the potential barrier domain selection.

For the density-gradient formulation, the Continuous Quasi-Fermi levels option is automatically satisfied with the Lagrange shape functions used for the quasi-Fermi level and Slotboom variables. This mimics the continuous nature of the quantum mechanical wave function, although it should be treated as phenomenology at the best (Ref. 47).

The Thermionic Emission option assumes the thermionic emission process dominates and allows the quasi-Fermi level and the Slotboom variable to be discontinuous across the heterojunction. The same formula as the drift-diffusion theory is used for the thermionic current density, yielding similar results.