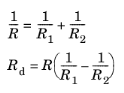Consider two solids having different radii of curvature in two tangential directions which are in point contact when no load is applied. Under the action of the load F, the contact area becomes elliptical. As a convention, let us assign the positive sign for the curvature of a convex surface and negative for a concave surface. The contact profile between the two solids A and B can be expressed in terms of the curvature sum,
R, and curvature difference,
Rd, as follows:
Indices 1 and
2 represent the local tangent directions.
R1 and
R2 are the effective radius of curvatures of the contacting surfaces in the local direction given by:
where ξ and
ζ are the elliptic integrals of first and second kind, respectively, defined as:
where δ is the penetration of the surfaces into each other.
When two cylindrical surfaces with parallel axes come in contact, the contact formed is a line contact. In this case, the force, F, changes the contact area into rectangular. The width of the contact area,
b, can be obtained in terms of the applied load,
F, equivalent radius of curvature,
R, and the effective elastic modulus,
E', as:
where L is the length of cylindrical surfaces in contact. The normal displacement is given by:
The derivative of the normal displacement, δ, with respect to the load,
F, gives the compliance. The inverse of the compliance is the stiffness of the contacting surfaces.
Figure 3-2 shows the front view of a typical roller bearing. Due to the relative motion of the inner race and outer race, some of the rollers get loaded, whereas others get unloaded. This relative motion determines the contact indentation at different rollers. From
Figure 3-3 the initial distance between the inner and outer race curvature centers is:
Let the relative center displacement between the inner and outer race be ur, and the relative tilt about local
y and
z directions be
θ2 and
θ3 respectively. Then the relative displacement between the inner and outer races at roller
i in row
j is:
for single row bearing. Here, b is the axial distance between the roller centers and
dp is the pitch diameter of the bearing. The loaded distance vector between the inner and outer race curvature centers is:
Introduce the displacement ui and rotation vector
θi at the reference point on the inner race, the displacement
ue and rotation vector
θe at the reference point on the outer race, and the displacement
ur and rotation vector
θr at the reference point on the rollers. Then, the displaced position
π of the arbitrary point located at
π0 from the reference point will be:
where uref and
θref are pair (
ui,
θi) for a point on the inner race, (
ue,
θe) for a point on the outer race and (
ur,
θr) for a point on the roller.
The compression δ at the contact between roller and raceway is found by taking the projection of the current relative position vectors of the nominal contact points on their outside normal vector and removing the initial gap:
where re and
ri are the position vectors on the outer and inner contact lines, respectively, with respect to the reference point.
dQe and
dQi are the infinitesimal forces acting on the infinitesimal length
dx on the outer and inner contact lines.
Here, eirj is the radial vector corresponding to the roller
i in row
j and is defined as:
Let the relative center displacement of the inner race with respect to outer race be ur and the relative tilt about local
y and
z directions be
θ2 and
θ3, respectively. Then the relative displacement of the inner with respect to outer races at roller
i in row
j is:
for a single row bearing. b is the axial distance between the roller centers and
dp is the pitch diameter of the bearing.
Here, Fa is the axial preload in the bearing,
e1 is the bearing axis,
ur is the rotor displacement,
uf is the foundation displacement and
er is the contact direction between the rolling element and the races. Because races of a bearing are connected to the rotor and the foundation, respectively, the displacement of the inner race is equal to the rotor displacement, and the displacement of the outer race is equal to foundation displacement. As you can see, for single row bearings, the preload is also transmitted to the rotor on which the bearing is mounted.
Let us assume that the outer race is split and that the part corresponding to the first row moves by an axial displacement ua along the bearing axis, and that the part corresponding to the second row moves by the same axial displacement but in opposite direction. The weak contribution due to the axial preload, in this case, is
We assume that radial deformation in the bearing is ur due to the preload. Then the weak contribution due to radial preload is
Fill angle: A fill angle ψf is the angular space occupied by the rolling elements on a pitch circle.
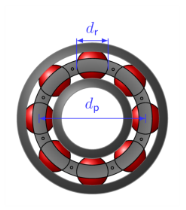
Since each rolling element has a diameter dr and there are
N number of them, the arc length occupied on the pitch circle by the rolling elements is
Ndr. Furthermore, the pitch circle radius is
dp/
2. Thus, the angular space occupied by the rollers, that is, the fill angle is
Inner race conformity: Inner race conformity, fin, is the ratio of the inner race radius of curvature to the diameter of the rolling element. It is defined by
Outer race conformity: Outer race conformity, fout, is the ratio of the outer race radius of curvature to the diameter of the rolling element. It is defined by
For a physical bearing, the fill angle cannot be larger than 2π radians. This gives a constraint on the diameter of the roller in relation to the pitch diameter as