Consider a space-fixed frame O and a body-fixed rotating frame
O* as shown in
Figure 3-1.
The origins of both frames coincide for all times t. The canonical basis vector triads for both frames are {
e1,
e2,
e3} and {
e1*,
e2*,
e3*}, respectively. Any vector
v in a basis can be expressed as
Therefore, basis vector triads in frame O*
can be expressed in terms of basis vectors in
O as
where the transformation matrix components are given by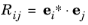 
. A component of a vector v as observed from the frame
O* can be written in terms of the components observed in
O as
Two frames will be considered: one is spatially fixed with its origin at xs and the other one is the body-fixed rotating frame with its origin at
xr. Points expressed in the body-fixed coordinates are distinguished from those represented in spatial coordinates by an asterisk (*) symbol. This means that if
x is a point in the spatial coordinate system, then
x∗ is the same point in the body-fixed coordinate system. Therefore, we can directly conclude that
xs =
0 and
xr∗ =
0. However,
xs∗ and
xr need not be zero. The relation between a space-fixed coordinate
x and body-fixed coordinate
x∗ can be expressed as
.