The Electromagnetic Wave Equation
The relationships between the electric and magnetic fields are together known as Maxwell’s Equations (Ref. 10),
where
•
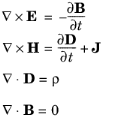
E (SI unit: V/m) is the electric field,
•
D (SI unit: C/m2) is the electric displacement,
•
H (SI unit: A/m) is the magnetic field,
•
B (SI unit: Wb/m2) is the magnetic flux density or magnetic induction,
•
ρ (SI unit: C/m3) is the charge density, and
•
J (SI unit: A/m2) is the current density.
The above equations are formulated in SI units. In Gaussian units (Ref. 9), the equations may be presented with additional factors of 4π and some additional divisions by the speed of light in a vacuum c.
The electric and magnetic quantities are further governed by the constitutive relations
where ε (SI unit: F/m) is the electric permittivity and μ (SI unit: H/m) is the magnetic permeability. Generally ε and μ are tensors of rank 2 but they can be treated as scalar quantities if the medium is isotropic.
In a medium that is charge-free, current-free, homogeneous, and isotropic, the first two of Maxwell’s Equations may be simplified to
One of the two remaining field variables can be eliminated by substitution, giving the so-called “curl-curl” equation for the remaining field,
If the medium is homogeneous, meaning it has spatially independent dielectric properties, then the factors of ε and μ can be taken outside the curl operator, and then using the identity
and recalling that the fields are divergence-free, the electromagnetic wave equation may be written as
Thus, either the electric field or magnetic field can be obtained by solving a vector Helmholtz equation. Here the electric field will be used.
The vector Helmholtz equation permits a variety of different solutions, one of which is a plane electromagnetic wave,
where
•
k (SI unit: rad/m) is the wave vector,
•
r (SI unit: m) is the position vector,
•
ω (SI unit: rad/s) is the angular frequency,
•
t (SI unit: s) is time, and
•
E0 (SI unit: V/m) is the complex-valued electric field amplitude at r = 0 and t = 0.
It is more common to express E as the exponential of a complex phase,
Although the real operator is not explicitly applied here, it should be understood that only the real part of this expression for E has any physical significance, and that the imaginary part is just a mathematical construction.
The form of the electric field is a set of plane surfaces of constant phase that propagate forward at the phase velocity
(3-3)
Where k is the magnitude of the wave vector k. This is the speed of light in the medium.
Differentiating E gives
However, since E is divergence-free, k and E must be orthogonal. The same can be deduced about k and H. In addition, from Maxwell’s Equations,
So that k, E, and H are all orthogonal.
Substituting the electromagnetic plane wave definition back into the electromagnetic wave equation yields
So the relationship between the angular frequency and wave vector norm is
(3-4)
Comparing Equation 3-3 and Equation 3-4 shows that
Now express the permittivity and permeability as
where
•
ε0 = 8.854187817 × 10-12 F/m is the vacuum permittivity,
•
μ0 = 1.256637062 × 10-6 H/m is the vacuum permeability,
•
εr (dimensionless) is the relative permittivity of the medium, and
•
μr (dimensionless) is the relative permeability of the medium.
Noting that
where c = 2.99792458 × 108 m/s is the speed of light in a vacuum, the phase velocity is
At optical frequencies, many materials are nonmagnetic, μr = 1. In that case, the phase velocity is just c/n, where
is the refractive index of the material. Thus, for linear nonmagnetic materials,
If the medium absorbs energy from the propagating wave or adds energy to it, then the refractive index becomes a complex-valued quantity, denoted n - iκ, where κ is called the extinction coefficient. For absorbing media, κ > 0, whereas for gain media, κ < 0.