Richards’ equation appears deceptively similar to the saturated flow equation set out in the Darcy’s Law interface, but it is notoriously nonlinear (Ref. 3). Nonlinearities arise because the material and hydraulic properties θl, Se, Cm, and κr vary for unsaturated conditions (for example, negative pressure) and reach a constant value at saturation (for example, pressure of zero or above). The volume of liquid per porous medium volume, θl, ranges from a small residual value θr to the total porosity εp. Its value is given in a constitutive relation in the model commonly defined as:

The variable θs is the saturated liquid volume fraction and therefore θs = εp. The effective saturation, Se has a maximum value of 1 at saturation and usually follows a nonlinear relationship if the porous medium is unsaturated. The specific moisture capacity, Cm, describes the change in θl as the solution progresses, the slope on a plot of θl versus pressure (or pressure head). The relative permeability, κr, increases with moisture content and varies from a nominal value to 1 at saturation, which reveals that the fluid moves more readily when the porous medium is fully wet.

The Richards’ Equation interface in COMSOL Multiphysics includes three retention models to define θl, Se, Cm, and κr:

The analytic formulas of van Genuchten (Ref. 4) and Brooks and Corey (Ref. 5) are so frequently used that they are synonymous with this variably saturated flow modeling. Posed in terms of pressure head Hp = p/(ρ g), the analytic expressions require data for the saturated θs and residual θr liquid volume fractions as well as constants α, n, m, and l, which specify a particular medium type.

The van Genuchten equations define saturation when the fluid pressure is atmospheric (that is, Hp = 0). For unsaturated conditions (Hp < 0) the effective saturation is defined as:

For the liquid volume fraction Equation 4-18 is used. The relative permeability is defined as

which results in κr = 1 at saturation (Se = 1). The specific moisture capacity is defined as:

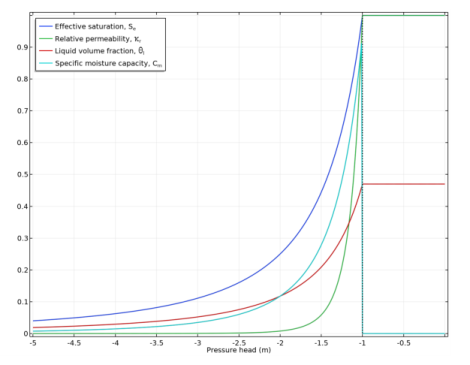
here, the constitutive parameter m is equal to 1 − 1 / n. The functions are highly nonlinear which is also depicted in Figure 4-2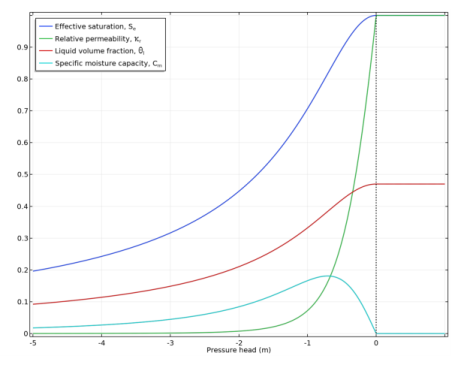

With the Brooks and Corey approach, an air-entry pressure distinguishes saturated (Hp > −1/α) and unsaturated (Hp < −1/α) flow so that

Again Equation 4-18 describes the liquid volume fraction. The relative permeability is defined as

which results in κr = 1 at saturation (Se = 1). The specific moisture capacity is defined as:

Here, the constitutive parameter m is equal to 1 − 1 / n. The functions are highly nonlinear which is also depicted in Figure 4-3

COMSOL Multiphysics also provides user-defined options for those who want to incorporate experimental data or arbitrary expressions to define these relationships. Enter expressions for θl, Se, Cm, and κr directly.