Theory for the Wall Boundary Condition

See Wall for the node settings.

The Slip condition assumes that there are no viscous effects at the slip wall and hence, no boundary layer develops. From a modeling point of view, this is a reasonable approximation if the important effect of the wall is to prevent fluid from leaving the domain. Mathematically, the constraint can be formulated as:

The no-penetration term takes precedence over the Neumann part of the condition and the above expression is therefore equivalent to

expressing that there is no flow across the boundary and no viscous stress in the tangential direction.

For a moving wall with translational velocity utr, u in the above equations is replaced by the relative velocity urel = u−utr.

Porous slip

The option, which can be chosen in the list when is activated, results in special treatment of boundaries and boundaries adjacent to porous domains ( feature). Namely, similar to the boundary condition, no penetration and tangential stress conditions are applied at the wall:

Here,

is the viscous wall traction,

is the wall normal,

is the tangential velocity at the wall while the real no slip is assumed to be at a distance

(half-height of the first cell adjacent to the wall) outside the wall, and

is the porous slip length. An analytical derivation of the velocity profile in the boundary layer where the pressure gradient is balanced by the sum of the Darcy term, Forchheimer drag, and a viscous term (neglecting convective terms) leads to the following expression for

where

is the porous length scale,

is the non-Darcian coefficient (

is the Forchheimer coefficient),

is the gravity vector, and

are intermediate variables. This formula is used when the is chosen and it reads pressure-gradient at the wall. By default, the is activated and the corresponding formula is:

Although this formulation is an approximation, since it uses slip velocity at the wall to reconstruct the pressure gradient, it is rather accurate. Moreover, the influence of convective terms is partially accounted for in this formulation.

Sliding Wall

The sliding wall option is appropriate if the wall behaves like a conveyor belt; that is, the surface is sliding in its tangential direction. The wall does not have to actually move in the coordinate system.

•

In 2D, the tangential direction is unambiguously defined by the direction of the boundary, but the situation becomes more complicated in 3D. For this reason, this boundary condition has slightly different definitions in the different space dimensions.

•

For 2D and 2D axisymmetric components, the velocity is given as a scalar Uw and the condition prescribes

where t = (ny , −nx) for 2D and t = (nz, −nr) for axial symmetry.

•

For 3D components, the velocity is set equal to a given vector uw projected onto the boundary plane:

The normalization makes u have the same magnitude as uw even if uw is not exactly parallel to the wall.

Navier Slip

This boundary condition enforces no-penetration at the wall,

, and adds a tangential stress

where

and K is the viscous stress tensor. β is a slip length, and

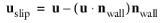
is the velocity tangential to the wall. The boundary condition does not set the tangential velocity component to zero; however, the extrapolated tangential velocity component is 0 at a distance β outside the wall.

The setting is per default set to . The slip length β is then defined as

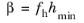
, where

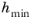
is the smallest element side (corresponds to the element size in the wall normal direction for boundary layer elements) and

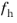
is a user input.

In cases where the wall movement is nonzero, may be selected to use

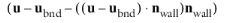
instead of

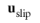
in the friction force. Then, the extrapolated tangential velocity component is

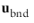
at a distance β outside of the wall. Note that the uw is always accounted for in the friction force.

The Navier Slip boundary condition is suitable for walls adjacent to a fluid-fluid interface or a free surface when solving for laminar flow. Applying this boundary condition, the contact line (fluid-fluid-solid interface) is free to move along the wall. Note that in problems with contact lines, the tangential velocity of the wall typically represents the movement of the contact line but the physical wall is not moving. In such cases, should not be checked.

Nonlinear Navier Slip

This boundary condition enforces no-penetration at the wall,

, and adds a tangential stress

where

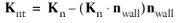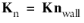and K is the viscous stress tensor. τref is a reference value used for scaling and dimensionalization and

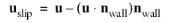
is the velocity tangential to the wall. The Nonlinear Navier Slip boundary condition is suitable for walls adjacent to a fluid-fluid interface or a free surface when solving for laminar flow. For further information, see the Navier Slip condition.

Hatzikiriakos Slip

When Hatzikiriakos slip is selected, a slip velocity is applied when the tangential stress is larger than the specified yield stress, τy,

where

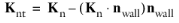and K is the viscous stress tensor. k1 (SI unit: m/s) and k2 (SI unit: 1/Pa) are the slip-velocity and compliance coefficients. Due to the exponential behavior in the slip velocity, the parameters τy, k1 and k2 need to be chosen carefully to avoid divergence of the numerical iterations. It is often advisable to start with the linear Navier slip model to get an estimate of the magnitude of the tangential stress.

In cases where the wall movement is nonzero, may be selected to set the slip velocity relative to the boundary velocity

. Note that the uw is always accounted for in the boundary velocity.

The Hatzikiriakos slip condition is suitable for walls adjacent to a fluid-fluid interface or a free surface when solving for laminar flow. Applying this boundary condition, the contact line (fluid-fluid-solid interface) is free to move along the wall. Note that in problems with contact lines, the tangential velocity of the wall typically represents the movement of the contact line but the physical wall is not moving. In such cases, should not be selected.

Asymptotic Slip

This boundary condition enforces no-penetration at the wall,

, and adds a tangential stress

where

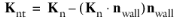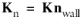and K is the viscous stress tensor. k1 (SI unit: m/s) and k2 (SI unit: 1/Pa) are the slip-velocity and compliance coefficients, while

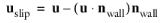
is the velocity tangential to the wall.

In cases where the wall movement is nonzero, may be selected to use

instead of

in the friction force.

The Asymptotic Slip boundary condition is suitable for walls adjacent to a fluid-fluid interface or a free surface when solving for laminar flow. Applying this boundary condition, the contact line (fluid-fluid-solid interface) is free to move along the wall. Note that in problems with contact lines, the tangential velocity of the wall typically represents the movement of the contact line but the physical wall is not moving. In such cases, should not be selected.

Constraint Settings

The wall feature uses three different techniques to constraint the velocity field:

•

Pointwise constraints is the standard technique to enforce strong constraints in the finite element method. The desired value of the velocity is prescribed at each node point in the mesh. Since the constraint is enforced locally at each node, only local values are affected by the constraint and the constraints are independent of each other. The solvers can therefore eliminate both the constrained degrees of freedom and the constraint force terms, effectively reducing the number of degrees of freedom being solved for.

The main advantage of pointwise constraints is that they enforce the constraint exactly pointwise. This means that they do not introduce any leakage of the velocity across the wall, unless specified. The main disadvantage of pointwise constraints is that they introduce locking effects when trying to impose a no-penetration condition for the velocity, u · n = 0, on curved walls or walls with sharp corners.

•

Using Weak constraints is an alternative method to prescribe the velocity. It consists on enforcing the boundary condition for the velocity via Lagrange multipliers. Their main advantage is that the Lagrange multiplier can provide an accurate representation of the reaction flux at the wall. Their main disadvantage is that they introduce extra unknowns, and are usually difficult to combine with other constraint methods on adjacent boundaries. Moreover, they may require extra constraints for the Lagrange multipliers. For more information, see Weak Constraints in the COMSOL Multiphysics Reference Manual.

•

Discontinuous Galerkin (DG) constraints use a numerical flux to prescribe the velocity at the wall. They impose the constraint in a integral sense rather than pointwise, and do not suffer from the locking effects introduced by pointwise constraints when trying to prescribe a no penetration condition for the velocity. They are also better behaved when prescribing nonlinear constraints. Their main disadvantage is that the constraint is only imposed approximately, and may produce small leaks. For more information, see Discontinuous Galerkin Formulation.

The following combination of Constraint techniques can be selected in the Constraint Setting sections of Wall boundary conditions:

•

Use default settings. The default settings use different constraint methods depending on whether only the normal component of the velocity is prescribed, such as in the no penetration condition, u · n = 0, imposed for example in Slip walls or No Slip walls using Wall Functions or Automatic Wall Treatment, or both tangential and normal components are prescribed, as is the case of No Slip walls in laminar flow.

DG constraints are used to impose the no penetration condition for Slip walls. When a No Slip condition is prescribed, pointwise constraints are used except for moving walls where DG constraints are used.

•

Use Pointwise constraints.

•

Use DG constraints.

•

Use Weak constraints. Weak constraints are not available on Interior Walls.

•

Use Mixed constraints. This option is only available when both the tangential and normal components of the velocity need to be prescribed. The velocity on the wall normal direction is imposed via pointwise constraints. The constraint for the tangential directions is relaxed, and DG constraints are used instead. This provides improved accuracy and performance when working with coarse boundary layer meshes. For more information, see Ref. 18.