Theory for Global Models

If the property is set to the model equations solved are greatly simplified because the spatial information of the different quantities in the plasma reactor are treated as volume-averaged. Without the spatial derivatives the numerical solution of the equation set becomes considerably simpler and the computational time is greatly reduced. This type of model is useful when investigating a broad region of parameters with complex plasma chemistries.

To avoid unnecessary complexity in the notation the same symbols which were used to represent the space-dependent quantities are used to represent the volume-averaged quantities. In the following the different densities, mass fractions and other quantities are to be thought as volume-averaged.

For a mixture consisting of k = 1, …, Q species and j = 1, …, N reactions the mass-fraction balance equations for the first Q − 1 species is given by

The sum in the last two term is over surfaces were species are lost or created. The forth term on the right hand side accounts for surface reactions of species kth. The last term on the right hand side is introduce because the species mass-balance equations are written in the nonconservative form and it is used the mass-continuity equation to replace for the mass density time derivative.

To take into account possible variations of the system total mass or pressure the mass-continuity equation can also be solved

The total feed mass-flow rate feeds is computed from

where QSCCM is the total mass flow given in number of SCCM units,

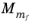
is the mean molar mass of the feed, and NStd is the standard number density computed at 1 atm and 273.15 K.

In the property it is possible to choose three different types of reactor models. If the is set to the mass-flow feeds are set to zero

and Equation 6-28 is solved to take into account possible mass changes in the system caused by surface reactions.

If the is set to the outlet mass-flow is set such that the feed and surface reactions cannot change the mass of the system

and the pressure in the reactor is found in order to keep the mass-density constant

If the is set to Equation 6-28 is not solved and the outlet mass-flow feed is set such that the mass feed and surface reactions cannot change the mass of the system

This condition ensures that the feed and surface reactions cannot change the mass density. However, the mass density can still change as a result of a change in the mean molar mass of the gas mixture in order to maintain a constant pressure.

A great part of a successful implementation of a plasma global modal depends on how the surface losses are estimated. For positive ions the forward rate constant can be estimate to be equal to the Bohm velocity

where Te is the electron temperature (V).

For neutral species the forward rate constant can be estimate by

When the correction option is set to

and when the correction option is set to , the forward rate constant is given via:

Equation 6-36 is an estimation of the diffusive losses to the wall where Λeff is the effective diffusion length, and Dk.m is the mixture-average diffusion coefficient of species k.

Surface reactions can be adjusted using the Correction factor hl. It is common practice to correct the surface ion losses by a factor that takes into account the ion spatial profile. Models for the ion correction factor can be found in literature Ref. 2 and Ref. 3.

The electron number density is obtained from electroneutrality

and electron energy density nε is computed from

where Pabs is the power absorbed by the electrons (SI unit: W), and e is the elementary charge. The last term on the right-hand side accounts for the kinetic energy transported to the surface by electrons and ions. The summation is over all positive ions and all boundaries with surface reactions, εe is the mean kinetic energy lost per electron lost, εi is the mean kinetic energy lost per ion lost, and Na is Avogadro’s number..
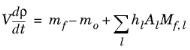