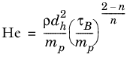You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Pipe Flow Interface calculates the pressure and velocity of an incompressible or weakly compressible fluid by solving the continuity and momentum equations outlined below.
(2-1)

(2-2)
The second term on the right-hand side in Equation 2-1 represents the pressure drop due to viscous shear. Here,
u is the cross-section averaged velocity (SI unit: m/s),
ρ the density (SI unit: kg/m
3),
p pressure (SI unit: Pa),
fD (dimensionless) the Darcy friction factor (see
Expressions for the Darcy Friction Factor) and
F is a volume force term (SI unit: N/m
3).
Furthermore, dh is the mean hydraulic diameter (SI unit: m), given by:
(2-3)
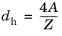
where A is the pipe cross section area (SI unit: m
2) available for flow, and
Z is the wetted perimeter (SI unit: m).
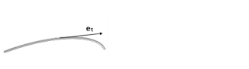
(2-4)
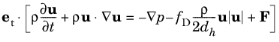
and we can define the tangential velocity u as
u = uet. The pipe flow physics interface in COMSOL Multiphysics
solves for the tangential velocity
u. This is also the quantity the user specifies in for example inflow boundary conditions and in the initial conditions settings.
The Darcy friction factor in Equation 2-1 accounts for the continuous pressure drop along a pipe segment due to viscous shear, and is expressed as a function of the Reynolds number (
Re) and the surface roughness divided by the hydraulic diameter (
e/dh).
(2-5)
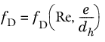
(2-6)
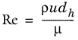
For single-phase fluids, the Churchill equation (Ref. 1) for the Darcy friction factor can be used for the full range of Re (laminar, transition and turbulent) and full range of
e/
d:
(2-7)

(2-8)
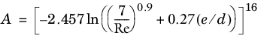
(2-9)
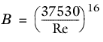
In the laminar regime (Re < 2000), fD is independent of the surface roughness and is given by the Stokes formula:
(2-10)
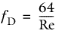
The Wood equation (Ref. 2) gives the friction factor for 4000 < Re < 1·10
7 and 1·10
-5 <
e/d < 0.04, according to
(2-11)

(2-12)
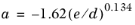
The Haaland equation (Ref. 3) for the Darcy friction factor is commonly used for oil pipelines and wells. It can recover both small and large relative roughness limits for a wide range of Reynolds numbers (4·10
3 < Re < 1·10
8)
(2-13)

(2-14)

For very low relative roughness e/d, the Haaland equation simplifies to Colebrook’s explicit formula (
Ref. 4)
(2-15)

For very large relative roughness e/d, the Haaland equation simplifies to the von Karman formula (
Ref. 5)
(2-16)
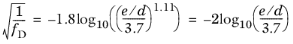
(2-17)
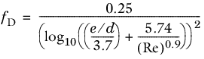
The equation is valid for relative roughness 1·10
-6 <
e/d < 1·10
-2 and for Reynolds number in the range 5·10
3 < Re < 1·10
8.
All the above equations are selectable from a list of friction factor expressions. As noted, only the Churchill equation covers both the laminar and turbulent flows, as well as the transitional region in between these flow regimes. The equations by Wood, Haaland, Colebrook, von Karman, or Swamee-Jain, intended for the turbulent regime, are combined with the Stokes equation for laminar flow to cover all flow conditions. When Re<1000, COMSOL Multiphysics selects Stokes equation if it predicts a friction factor greater than equations for the turbulent regimes. This produces more accurate results that using the turbulent frictions factors in the laminar regime, but it does not necessarily produce accurate estimates of the friction factor in the transition region. Therefore, it is always advisable to check the Reynolds number for a give pipe flow solution and change the friction model and recalculate, if necessary.
The Newtonian fluid type also has two Gas-Liquid options, which employs a simple two-phase approach presented by Balasubramaniam and others (
Ref. 26). This is a one-fluid approach that treats the fluid as one phase (one mass and momentum balance is solved), but it corrects the pressure drop correlation with empirical factors for liquid-gas mixtures. As such, the model also makes the following assumptions:
The first selectable method is the gas-liquid, friction factor multiplier, which modifies the single-phase Newtonian Darcy friction factor defined in
Equation 2-7 and on, such that
(2-18)
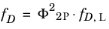
where fD,L is the Newtonian single phase friction factor computed as described earlier in this section.
fD is then used as usual in the pressure drop correlation in
Equation 2-4. The two-phase friction factor
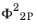
is calculated as (
Ref. 26)
(2-19)
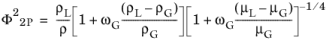
where ρL,
μL,
ρG, and
μG are the density and viscosity of the liquid, and gas, respectively, and where
ωG is the quality (the gas phase mass fraction). The total density in
Equation 2-19 is calculated as
(2-20)
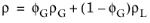
(2-21)
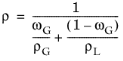
(2-22)
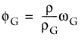
The second selectable gas-liquid method is the gas-liquid, effective Reynolds number. This method uses an effective adjusted viscosity to calculate the Reynolds number in the pressure loss calculations. The default mixture viscosity model is the extended Einstein, which probably is the most accurate within a large range of gas mass fractions (
Ref. 27):
(2-23)
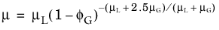
(2-24)
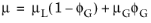
(2-25)
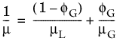
(2-26)
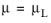
where mp and
n are two empirical curve fitting parameters known as the fluid consistency coefficient and the flow behavior index, respectively. Note that the dimensions of the consistency coefficient,
mp, depend on value of the value of
n. The power law relation can be written as
(2-27)
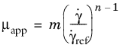
Here 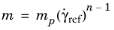 is the value of apparent viscosity at the reference share rate
is the value of apparent viscosity at the reference share rate 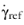 . The reference shear rate
. The reference shear rate  has the default value 1 s-1
has the default value 1 s-1. In the laminar regime the friction factor for power law fluids can be calculated by the Stokes equation using the modified Reynolds number proposed by Metzner and Reed (
Ref. 7):
(2-28)
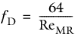
(2-29)
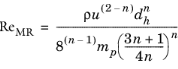
For the turbulent regime Irvine (Ref. 8) proposed the following expression for the friction factor:
(2-30)
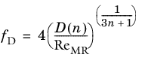
(2-31)

Ryan and Johnson (Ref. 9) formulated a criterion for the transition between laminar and turbulent flow, where
(2-32)
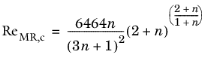
(2-33)

The yield stress, τB (SI unit: Pa), and the plastic viscosity,
μB (SI unit: Pa·s), are found by curve fitting to experimental data.
The Swamee-Aggarwal equation (Ref. 10) gives the friction factor for a Bingham plastic fluid in the laminar regime according to:
(2-34)

(2-35)

(2-36)
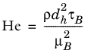
(2-37)
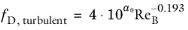
(2-38)
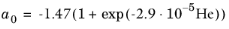
(2-39)
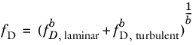
(2-40)
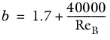
(2-41)

The yield stress, τB (SI unit: Pa), and the consistency coefficient,
m (SI unit: Pa·s), and flow behavior index,
n are found by curve fitting to experimental data.
The Swamee-Aggarwal equation (Ref. 12) gives the friction factor for a Heschel-Bukley fluid in the laminar regime according to:
(2-42)

(2-43)