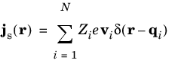Given an array of idealized point sources such that the position vector of the ith source is denoted
qi (SI unit: m), the contribution to the current density by particles
js at position
r is
For example, instead of allocating degrees of freedom for 1012 electrons, it will often suffice to model 10
4 particles, each of which has a
Charge multiplication factor of 10
8, meaning that it represents 10
8 electrons.
The treatment of particle beams as constant-current beams is determined by the Particle release specification list in the settings window for the Charged Particle Tracing physics interface. If
Specify release times is selected, the charge density is computed using
Equation 6-11 and is determined by the instantaneous positions of all model particles. Thus, it is necessary to solve for the particle trajectories, electric potential, and magnetic vector potential in the time domain. If
Specify current is selected, the current density is computed using
Equation 6-12 and is determined by the time history of the model particle positions.
The difference between the Specify current and
Specify release times particle release specifications is thus analogous to the difference between integration over
Elements and time and integration over
Elements as described for the
Accumulator (Domain) node.
At this point, the effect of a bidirectional coupling between the particle trajectories and fields has not been considered. If Specify release times is selected from the
Particle release specification list, this does not require special consideration because the trajectories and fields are computed simultaneously. If
Specify current is selected, however, the trajectories and fields are computed using different study types, and an additional feedback mechanism is needed. The
Bidirectionally Coupled Particle Tracing study step generates a solver sequence that does the following:
The Magnetic Particle Field Interaction node defines a variable for each component of the contribution to the current density by particles in each mesh element. This variable is discretized using constant shape functions. For a mesh element
j with volume
Vj, and with the
Particle release specification set to
Specify release times, the average current density
ρj is
where ni (dimensionless) is the charge multiplication factor of the
ith model particle. The integral on the right-hand side is a volume integral over element
j. The resulting current density is the average current density over the mesh element, which may be written as
If instead the Particle release specification is
Specify current, each model particle represents a number of particles per unit time which follow along the same path, determined by the effective frequency of release
frel. Then the time derivative of the current density can be expressed as