
|
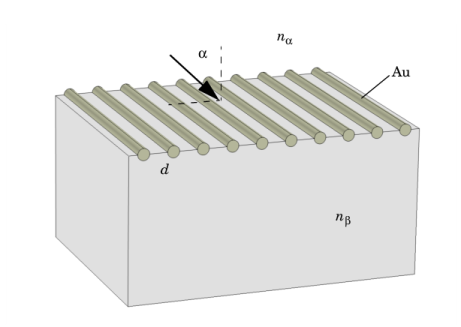
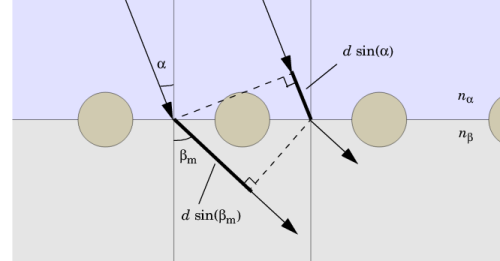
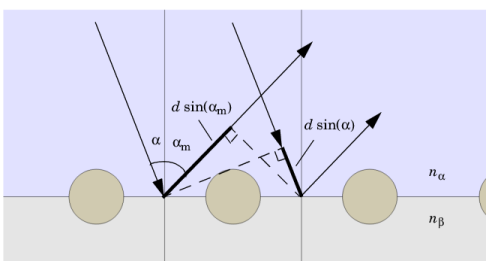

|
1
|
|
2
|
In the Select Physics tree, select Optics>Wave Optics>Electromagnetic Waves, Frequency Domain (ewfd).
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
7
|
Click
|
|
8
|
|
9
|
|
10
|
|
11
|
Click Replace.
|
|
12
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select all objects.
|
|
3
|
|
1
|
|
2
|
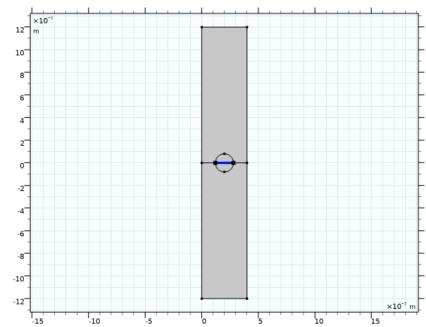
On the object uni1, select Boundary 6 only. This is the horizontal diameter of the circle in the center of the geometry.
 |
|
3
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
In the tree, select Optical>Inorganic Materials>Au - Gold>Models and simulations>Au (Gold) (Rakic et al. 1998: Brendel-Bormann model; n,k 0.248-6.20 um), to select gold from the Optical Materials Database.
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
Clear the Include in automatic diffraction order calculation check box, to not remove the manually added Diffraction Order port subfeatures below this port when you later will click the Add Diffraction Orders button.
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kIncx_1,ewfd.kIncy_1 - Incident wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Incident wave (magenta).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_1,ewfd.kModey_1 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Reflected wave (blue).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_2,ewfd.kModey_2 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Transmitted wave (blue).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_3,ewfd.kModey_3 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Reflected mode, m = -1 (cyan).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_4,ewfd.kModey_4 - Port mode wave vector.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Arrow Line 4 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Arrow Line 5 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Results click Reflectance, Transmittance, and Absorptance (ewfd).
|
|
2
|
In the Settings window for 1D Plot Group, type TE Reflectance, Transmittance, and Absorptance in the Label text field.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the TE Reflectance, Transmittance, and Absorptance node, then click Global 1.
|
|
2
|
|
3
|
|
4
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Electromagnetic Waves, Frequency Domain (ewfd) click Port 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
Locate the Automatic Diffraction Order Calculation section. Click Add Diffraction Orders, to update the Diffraction Order port subfeatures below Port 2.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Electromagnetic Waves, Frequency Domain (ewfd) click Port 2.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Wavelength Domain.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|
|
6
|
Click
|
|
7
|
|
8
|
|
9
|
|
10
|
Click Replace.
|
|
11
|
|
13
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kIncx_1,ewfd.kIncy_1 - Incident wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Incident wave (magenta).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_1,ewfd.kModey_1 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Reflected wave (blue).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_2,ewfd.kModey_2 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Transmitted wave (blue).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_3,ewfd.kModey_3 - Port mode wave vector.
|
|
3
|
|
4
|
|
5
|
In the associated text field, type Reflected mode, m = -1 (cyan).
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>ewfd.kModex_4,ewfd.kModey_4 - Port mode wave vector.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Arrow Line 4 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Results>Electric Field (ewfd) right-click Arrow Line 5 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Results click Reflectance, Transmittance, and Absorptance (ewfd).
|
|
2
|
In the Settings window for 1D Plot Group, type TM Reflectance, Transmittance, and Absorptance in the Label text field.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, expand the TM Reflectance, Transmittance, and Absorptance node, then click Global 1.
|
|
2
|
|
3
|
|
4
|
|
6
|