PDF
Band-Gap Analysis of a Photonic Crystal
This application performs a band-gap analysis of a photonic crystal similar to the one used in the Photonic Crystal model.
Introduction
The model investigates the wave propagation in a photonic crystal that consists of GaAs pillars placed equidistant from each other. The distance between the pillars determines a relationship between the wave number and the frequency of the light that prevents light of certain wavelengths to propagate inside the crystal structure. This frequency range is called the photonic band gap (Ref. 2). There are several band gaps for a certain structure, and this application extracts the band gaps for the lowest bands of the crystal.
Model Definition
This application is similar to the Photonic Crystal waveguide model. The difference is that in this application the crystal itself is analyzed instead of a waveguide. Because it has a repeated pattern it is possible to use periodic boundary conditions. As a result, only one pillar is needed for this simulation.
There are two main complications with this band-gap analysis. Firstly, the refractive index of GaAs is frequency dependent. Secondly, the wave vector must be ramped for the band diagram. Although you can solve each of these complications with the eigenvalue solver separately, the two complications combined make it difficult without reformulating the problem. Thus, formulate a nonlinear eigenvalue problem, using a stationary solver with the eigenvalue as an unknown. The equation for the eigenvalue is a normalization of the electric field, so the average field is unity over the domain. The nonlinear solver finds the correct eigenvalue with an updated refractive index to the found eigenvalue. Furthermore, the parametric solver can sweep the wave vector, k.
The wave vector for the propagating wave, k, enters the simulation as Floquet periodicity boundary conditions (Ref. 1),
where β is a phase factor determined by the wave vector and the distance, d, between the periodic boundaries:
The range for the swept k is determined by the reciprocal lattice vectors of the photonic crystal, and these are determined from the primitive lattice vectors. For a 2D crystal there are two lattice vectors, a1 and a2, defined in Figure 1.
Figure 1: Definition of the square primitive cells and the lattice vectors a1 and a2.
The reciprocal lattice vectors are calculated from a1 and a2 using the relations
where a3 is assumed to be the unit vector ez. When a1 and a2 are perpendicular to each other and to a3, b1 and b2 become
Results and Discussion
Figure 2 shows the z-component of the electric field, as determined by the eigenfrequency solver for k=0.
Figure 2: Z-component of the electric field for k = 0.
Figure 3 shows the z-component of the electric field for k=0.5 for the fifth band, as determined by the nonlinear solver.
Figure 3: Z-component of the electric field for the fifth band and k = 0.5.
Finally, Figure 4 shows the band diagram for k swept from 0 to 0.5 in the (1,1) direction. Notice that band two and three are degenerate for k=0, and that band one and two and four and five are degenerate at k=0.5.
Between band three and four there is a frequency range for which there are no states. This frequency range corresponds to a band gap in the structure, as there can be no propagating waves in the (1,1) propagation direction for that frequency range.
Notice that there is actually a band with a lower frequency than for the lowest band in Figure 4. However, this band has so small frequencies that the approximation for the frequency-dependent refractive index of GaAs is no longer valid. Thus, this band has not been included in the calculations.
Figure 4: The dispersion relation (frequency versus wave number), when the wave vector is varied in the direction (1,1), for the five lowest bands.
Notes About the COMSOL Implementation
One catch with the nonlinear formulation is that the mode normalization performed by the global equation involves setting the domain integral of Ez*conj(Ez) to unity. However, the conjugate function is non-analytical in complex mathematics sense so a correct Jacobian cannot be obtained by the nonlinear solver.
To obtain a correct Jacobian, COMSOL’s complex splitting functionality is used. Thereby COMSOL internally splits complex entities into the constituent real and imaginary parts. Thus, the problem is converted from a complex-valued problem to a real-valued problem that is fully differentiable. After solution, COMSOL translates the solution back into complex form.
The complex splitting makes the problem solve faster and more robustly.
References
1. C. Kittel, Introduction to Solid State Physics, 7th ed., John Wiley & Sons, New York, 1996.
2. J.D. Joannopoulus, R.D. Meade, and J.N. Winn, Photonic Crystals (Modeling the Flow of Light), Princeton University Press, 1995.
Application Library path: Wave_Optics_Module/Gratings_and_Metamaterials/bandgap_photonic_crystal
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D.
2
In the Select Physics tree, select Optics>Wave Optics>Electromagnetic Waves, Frequency Domain (ewfd).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Eigenfrequency.
6
Click  Done.
Global Definitions
Parameters 1
First add parameters, characterizing the geometry of the periodic cell.
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
a
375[nm]
3.75E-7 m
Primitive cell side length
b
70[nm]
7E-8 m
GaAs pillar radius
k
0
0
Fraction of wave vector magnitude
k1
1
1
First component of wave direction vector
k2
1
1
Second component of wave direction vector
a1x
a
3.75E-7 m
First lattice vector, x component
a1y
0[nm]
0 m
First lattice vector, y component
a2x
0[nm]
0 m
Second lattice vector, x component
a2y
a
3.75E-7 m
Second lattice vector, y component
band
1
1
Band number
The last parameter, band, will be used for selecting what band to calculate the dispersion relation for.
Definitions
Variables 1
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
Add variables representing the reciprocal lattice vector and the Floquet wave vector (used later in the periodic boundary condition).
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
b1x
2*pi*a2y/(a1x*a2y-a1y*a2x)
1/m
First reciprocal lattice vector, x component
b1y
-2*pi*a2x/(a1x*a2y-a1y*a2x)
1/m
First reciprocal lattice vector, y component
b2x
-2*pi*a1y/(a1x*a2y-a1y*a2x)
1/m
Second reciprocal lattice vector, x component
b2y
2*pi*a1x/(a1x*a2y-a1y*a2x)
1/m
Second reciprocal lattice vector, y component
kx
k*(k1*b1x+k2*b2x)
1/m
Floquet vector, x component
ky
k*(k1*b1y+k2*b2y)
1/m
Floquet vector, y component
Geometry 1
The geometry consists of a square air cell surrounding a circular GaAs pillar.
Square 1 (sq1)
1
In the Geometry toolbar, click  Square.
2
In the Settings window for Square, locate the Size section.
3
In the Side length text field, type a.
4
Locate the Position section. From the Base list, choose Center.
Circle 1 (c1)
1
In the Geometry toolbar, click  Circle.
2
In the Settings window for Circle, locate the Size and Shape section.
3
In the Radius text field, type b.
4
Click  Build All Objects.
5
Click the  Zoom Extents button in the Graphics toolbar.
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
Define the air, that will surround the GaAs pillar.
3
In the tree, select Built-in>Air.
4
Click Add to Component in the window toolbar.
5
In the Home toolbar, click  Add Material to close the Add Material window.
Definitions
Analytic 1 (an1)
1
In the Home toolbar, click  Functions and choose Global>Analytic.
The dispersion relation for the refractive index of GaAs will be used in more than one place, so it is best to define it as an analytical function.
2
In the Settings window for Analytic, type n_GaAs in the Function name text field.
3
Locate the Definition section. In the Expression text field, type -3.3285e5[1/m]*c_const/f+3.8359.
4
In the Arguments text field, type f.
5
Locate the Units section. In the table, enter the following settings:
Argument
Unit
f
Hz
6
In the Function text field, type 1.
Electromagnetic Waves, Frequency Domain (ewfd)
Compute the solution for out-of-plane polarization.
1
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
2
In the Settings window for Electromagnetic Waves, Frequency Domain, locate the Components section.
3
From the Electric field components solved for list, choose Out-of-plane vector.
Periodic Condition 1
1
In the Physics toolbar, click  Boundaries and choose Periodic Condition.
Define the periodic boundary conditions, using the Floquet wave vector.
2
Click the  Zoom Extents button in the Graphics toolbar.
3
Select Boundaries 1 and 4 only.
4
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
5
From the Type of periodicity list, choose Floquet periodicity.
6
Specify the kF vector as
kx
x
ky
y
Periodic Condition 2
1
In the Physics toolbar, click  Boundaries and choose Periodic Condition.
2
Select Boundaries 2 and 3 only.
3
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
4
From the Type of periodicity list, choose Floquet periodicity.
5
Specify the kF vector as
kx
x
ky
y
Add a wave equation feature, representing the GaAs pillar.
Wave Equation, Electric 2
1
In the Physics toolbar, click  Domains and choose Wave Equation, Electric.
2
Select Domain 2 only.
3
In the Settings window for Wave Equation, Electric, locate the Electric Displacement Field section.
4
From the n list, choose User defined. In the associated text field, type n_GaAs(freq).
5
From the k list, choose User defined.
Mesh 1
1
In the Model Builder window, under Component 1 (comp1) click Mesh 1.
2
In the Settings window for Mesh, locate the Physics-Controlled Mesh section.
3
From the Element size list, choose Finer.
Define the mesh so that the meshes on opposite edges are identical. This is important for the periodic boundary conditions, so that the source and destination meshes are the same.
Edge 1
1
In the Mesh toolbar, click  Edge.
2
Select Boundaries 1 and 2 only.
Copy Edge 1
1
In the Model Builder window, right-click Mesh 1 and choose Copying Operations>Copy Edge.
2
Select Boundary 1 only.
3
In the Settings window for Copy Edge, locate the Destination Boundaries section.
4
Click to select the  Activate Selection toggle button.
5
Select Boundary 4 only.
Copy Edge 2
1
Right-click Mesh 1 and choose Copying Operations>Copy Edge.
2
Select Boundary 2 only.
3
In the Settings window for Copy Edge, locate the Destination Boundaries section.
4
Click to select the  Activate Selection toggle button.
5
Select Boundary 3 only.
Free Triangular 1
1
In the Mesh toolbar, click  Free Triangular.
2
In the Settings window for Free Triangular, click  Build All.
Study 1
Step 1: Eigenfrequency
Find the eigenfrequencies, for k = 0, around 550 THz.
1
In the Model Builder window, under Study 1 click Step 1: Eigenfrequency.
2
In the Settings window for Eigenfrequency, locate the Study Settings section.
3
Select the Desired number of eigenfrequencies check box.
4
In the associated text field, type 5.
5
In the Search for eigenfrequencies around text field, type 550[THz].
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
Define the Transform point to the initial eigenfrequency guess, to make sure that a zero frequency will not be assigned to the denominator in any expression.
2
In the Model Builder window, expand the Solution 1 (sol1) node, then click Eigenvalue Solver 1.
3
In the Settings window for Eigenvalue Solver, locate the General section.
4
In the Value of eigenvalue linearization point text field, type 550[THz].
5
In the Study toolbar, click  Compute.
Results
Electric Field (ewfd)
Visualize the z component of the electric field, deforming the surface using a height expression.
Surface 1
1
In the Model Builder window, expand the Electric Field (ewfd) node, then click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type ewfd.Ez.
Height Expression 1
1
Right-click Surface 1 and choose Height Expression.
2
Click the  Zoom Extents button in the Graphics toolbar. Compare the results with Figure 2.
Component 1 (comp1)
To find the frequencies for the nonzero wave vectors, solve for the frequency using a nonlinear state equation, requiring the field to be normalized in the unit cell, and a second wave equation.The solution from the first wave equation is used as the initial value for the second wave equation.
Add Physics
1
In the Home toolbar, click  Add Physics to open the Add Physics window.
2
Go to the Add Physics window.
3
In the tree, select Mathematics>ODE and DAE Interfaces>Global ODEs and DAEs (ge).
4
Click Add to Component 1 in the window toolbar.
5
In the tree, select Recently Used>Electromagnetic Waves, Frequency Domain (ewfd).
6
Click Add to Component 1 in the window toolbar.
7
In the Home toolbar, click  Add Physics to close the Add Physics window.
Global ODEs and DAEs (ge)
Global Equations 1
1
In the Model Builder window, under Component 1 (comp1)>Global ODEs and DAEs (ge) click Global Equations 1.
2
In the Settings window for Global Equations, locate the Global Equations section.
3
In the table, enter the following settings:
Name
f(u,ut,utt,t) (1)
Initial value (u_0) (1)
Initial value (u_t0) (1/s)
Description
freq1
1[V^2/m^2]-nEz
-imag(lambda)/(2*pi)
0
Frequency
Here, the initial value for the frequency freq1 is taken from the eigenvalue from the initial eigenfrequency analysis.
4
Locate the Units section. Click  Select Dependent Variable Quantity.
5
In the Physical Quantity dialog box, type frequency in the text field.
6
Click  Filter.
7
In the tree, select General>Frequency (Hz).
8
Click OK.
9
In the Settings window for Global Equations, locate the Units section.
10
Click  Define Source Term Unit.
11
In the Source term quantity table, enter the following settings:
Source term quantity
Unit
Custom unit
V^2/m^2
Electromagnetic Waves, Frequency Domain 2 (ewfd2)
1
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain 2 (ewfd2).
2
In the Settings window for Electromagnetic Waves, Frequency Domain, click to expand the Equation section.
The frequency used by this interface is the one solved for with the state equation, freq1.
3
From the Equation form list, choose Frequency domain.
4
From the Frequency list, choose User defined. In the f text field, type freq1.
5
Locate the Components section. From the Electric field components solved for list, choose Out-of-plane vector.
Initial Values 1
Assign the initial value to the solution from the initial eigenfrequency analysis. As more than one eigenfrequency solution was found, you will later specify, for the Stationary study step, which of the eigenfrequency solutions to select for the initial value.
1
In the Model Builder window, under Component 1 (comp1)>Electromagnetic Waves, Frequency Domain 2 (ewfd2) click Initial Values 1.
2
In the Settings window for Initial Values, locate the Initial Values section.
3
Specify the E2 vector as
0
x
0
y
ewfd.Ez
z
Periodic Condition 1
1
In the Physics toolbar, click  Boundaries and choose Periodic Condition.
2
Select Boundaries 1 and 4 only.
3
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
4
From the Type of periodicity list, choose Floquet periodicity.
5
Specify the kF vector as
kx
x
ky
y
Periodic Condition 2
1
In the Physics toolbar, click  Boundaries and choose Periodic Condition.
2
Select Boundaries 2 and 3 only.
3
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
4
From the Type of periodicity list, choose Floquet periodicity.
5
Specify the kF vector as
kx
x
ky
y
Wave Equation, Electric 2
1
In the Physics toolbar, click  Domains and choose Wave Equation, Electric.
2
Select Domain 2 only.
3
In the Settings window for Wave Equation, Electric, locate the Electric Displacement Field section.
4
From the n list, choose User defined. In the associated text field, type n_GaAs(freq1). Notice that it must be the frequency freq1 that is used here.
5
From the k list, choose User defined.
Definitions
Define the integration operator, used for the normalization of the field.
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
Click in the Graphics window and then press Ctrl+A to select both domains.
Variables 1
Add the variables that define the normalization of the field.
1
In the Model Builder window, click Variables 1.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
A
intop1(1)
m²
Area
nEz
intop1(realdot(ewfd2.Ez,ewfd2.Ez))/A
kg²·m²/(s6·A²)
Normalization integral
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Some Physics Interfaces>Stationary.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Stationary
The stationary study will not include the first interface (ewfd).
1
In the Settings window for Stationary, locate the Physics and Variables Selection section.
2
In the table, clear the Solve for check box for Electromagnetic Waves, Frequency Domain (ewfd).
Select what eigenfrequency solution for the first Electromagnetic Waves, Frequency Domain interface (ewfd) that will be used as the initial value to the second Electromagnetic Waves, Frequency Domain (ewfd2) interface.
3
Click to expand the Values of Dependent Variables section. Find the Initial values of variables solved for subsection. From the Settings list, choose User controlled.
4
From the Study list, choose Study 1, Eigenfrequency.
5
From the Eigenfrequency list, choose Manual.
6
In the Index text field, type band.
7
Click to expand the Study Extensions section. Select the Auxiliary sweep check box.
8
Click  Add.
Scan the fraction of the wave vector magnitude from 0 to 0.5 (half the Brillouin zone).
9
From the list in the Parameter name column, choose k (Fraction of wave vector magnitude).
10
Click  Range.
11
In the Range dialog box, type 0 in the Start text field.
12
In the Step text field, type 0.01.
13
In the Stop text field, type 0.5.
14
Click Replace.
Solution 2 (sol2)
1
In the Study toolbar, click  Show Default Solver.
Solve the stationary problem using complex splitting, to split the complex expressions into their real and imaginary parts. Thereby the expressions become analytical and an exact Jacobian can be calculated.
2
In the Model Builder window, expand the Solution 2 (sol2) node, then click Compile Equations: Stationary.
3
In the Settings window for Compile Equations, locate the Study and Step section.
4
Select the Split complex variables in real and imaginary parts check box.
Global ODEs and DAEs (ge)
Global Equations 1
1
Click the  Show More Options button in the Model Builder toolbar.
2
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Advanced Physics Options.
3
Click OK.
4
In the Model Builder window, under Component 1 (comp1)>Global ODEs and DAEs (ge) click Global Equations 1.
5
In the Settings window for Global Equations, click to expand the Discretization section.
6
From the Value type when using splitting of complex variables list, choose Real, as the frequency freq1 has no imaginary part.
Study 2
Add a parametric sweep to calculate the dispersion relations for the five lowest bands.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
From the list in the Parameter name column, choose band (Band number).
5
Click  Range.
6
In the Range dialog box, type 1 in the Start text field.
7
In the Step text field, type 1.
8
In the Stop text field, type 5.
9
Click Replace.
Solution 2 (sol2)
1
In the Model Builder window, expand the Study 2>Solver Configurations>Solution 2 (sol2)>Stationary Solver 1 node, then click Parametric 1.
2
In the Settings window for Parametric, click to expand the Continuation section.
3
Select the Tuning of step size check box, to make sure the solver takes small enough steps when starting the sweep.
4
In the Initial step size text field, type 0.0001.
5
In the Minimum step size text field, type 0.0001.
6
In the Maximum step size text field, type 0.01.
7
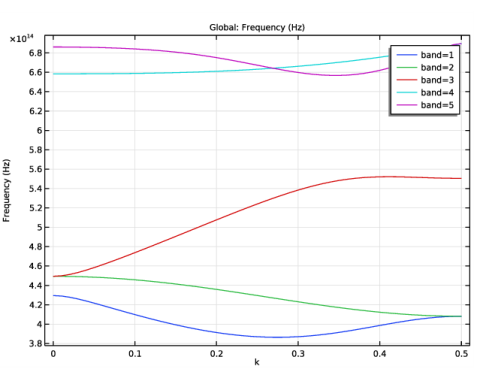
From the Predictor list, choose Constant. This makes the solver first try with the solution found for the previously calculated k value. This is preferred, as even though the states can be degenerate, the field solutions are orthogonal. Thus, the solver is forced to follow the right band.
8
In the Study toolbar, click  Compute.
Results
Surface 1
1
In the Model Builder window, expand the Electric Field (ewfd2) node, then click Surface 1.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type ewfd2.Ez.
Height Expression 1
1
Right-click Surface 1 and choose Height Expression.
Modify the phase for the dataset to make the plot look better.
Study 2/Parametric Solutions 1 (sol3)
1
In the Model Builder window, expand the Results>Datasets node, then click Study 2/Parametric Solutions 1 (sol3).
2
In the Settings window for Solution, locate the Solution section.
3
In the Solution at angle (phase) text field, type 180.
Height Expression 1
Click the  Zoom Extents button in the Graphics toolbar. Compare the results with Figure 3.
Study 2/Parametric Solutions 1 (sol3)
Before making the final plot, reset the phase for the dataset. Otherwise the frequencies will be plotted with a negative sign. You could also prevent the sign change by plotting freq1*exp(-j*root.phase), instead of plotting just freq1.
1
In the Model Builder window, under Results>Datasets click Study 2/Parametric Solutions 1 (sol3).
2
In the Settings window for Solution, locate the Solution section.
3
In the Solution at angle (phase) text field, type 0.
1D Plot Group 3
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 2/Parametric Solutions 1 (sol3).
Global 1
1
Right-click 1D Plot Group 3 and choose Global.
2
In the Settings window for Global, click to expand the Legends section.
3
From the Legends list, choose Manual.
4
In the table, enter the following settings:
Legends
band=1
band=2
band=3
band=4
band=5
5
In the 1D Plot Group 3 toolbar, click  Plot. Compare the results with Figure 4.