
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
From the Geometry representation list, choose CAD kernel. This is necessary because the prepared geometry sequence contains a Fillet feature.
|
|
4
|
|
5
|
Browse to the model’s Application Libraries folder and double-click the file bracket_uncertainty_quantification_fillet_geom_sequence.mph.
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
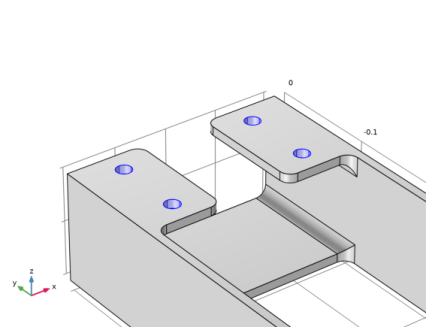
Select the Group by continuous tangent check box. This setting greatly facilitates the selection of curved surfaces. In this case use it to select the four bolt holes. It is sufficient to select one boundary per hole; the three other boundaries will be selected automatically.
 |
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click OK.
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Solid Mechanics (solid) and choose Fixed Constraint.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
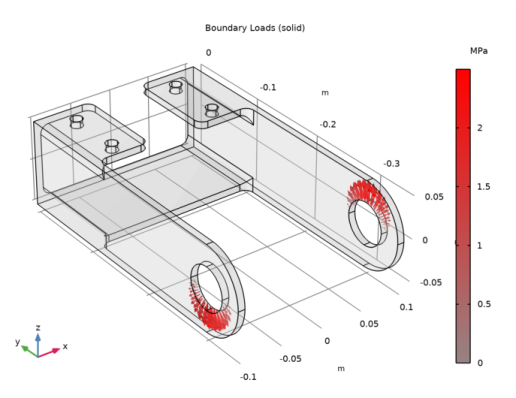
In the Model Builder window, expand the Applied Loads (solid) node, then click Boundary Loads (solid).
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
Click
|
|
5
|
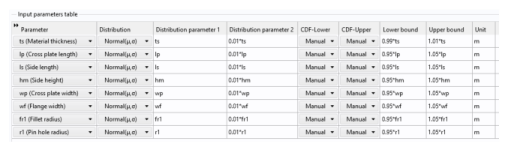
Locate the Input Parameters section. Find the Input parameters table subsection. Click
|
|
7
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Uncertainty Quantification, locate the Uncertainty Quantification Settings section.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Find the Input parameters table subsection. Ctrl-click to select table rows 1, 2, 4, and 6–8. This is most easily done by first clicking in the table’s upper-left corner and then dragging the bottom border of the pop-out table downward until you see all rows at once. The rows to select are those for the parameters ts, lp, hm, wf, fr1, and r1.
|
|
4
|
Click
|
|
5
|
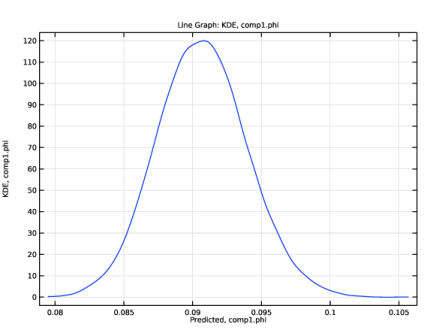
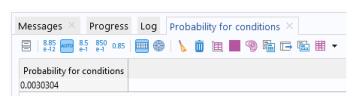
Locate the Uncertainty Quantification Settings section. From the Compute action list, choose Compute and analyze. The default Compute action is Improve and analyze. This will reuse the previously computed uncertainty quantification results in order to speed up the computation. However, we are changing to Compute and analyze, which is slower, but gives a higher-fidelity result.
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
Locate the Surrogate-Based Response Surface section. Click Response Surface in the upper-right corner of the section.
|