You are viewing the documentation for an older COMSOL version. The latest version is available here.
PDF
Bracket — Linear Buckling Analysis
Introduction
Buckling analysis is an important study type in structural mechanics because it provides an estimate of the critical load that can cause sudden collapse of the structure. In this example, you first learn how to perform a linear buckling analysis to find the critical buckling load. In a second study, you will compute the nonlinear deformation while increasing the applied load until buckling occurs.
It is recommended you review the Introduction to the Structural Mechanics Module, which includes background information and discusses the bracket_basic.mph model relevant to this example.
Model Definition
This model is an extension of the example described in the section “The Fundamentals: A Static Linear Analysis” in the Introduction to the Structural Mechanics Module.
The analysis computes the critical compressive load with a load vector resultant oriented in the positive y direction in one of the arms of the bracket.
Results and Discussion
Figure 1 shows the first buckling mode for the bracket geometry. The critical load factor is about 6·104, which corresponds to the critical buckling load 60 kN since the static load used is 1 N.
Figure 1: First buckling mode and critical load factor value.
Figure 2 shows the solution from the nonlinear analysis. The variation of the displacement in the right arm of the bracket is plotted as function of increasing applied load (blue). You can see how the displacement deviates strongly from the linear response as the applied load approaches the critical buckling load from the linear buckling analysis. A deviation of 20% from linearity is obtained at an applied force of 57 kN.
Figure 2: Bracket right arm y-displacement versus applied load.
Notes About the COMSOL Implementation
In a linear buckling analysis, you perform the following operations:
•
Run a linear static analysis using a load of arbitrary magnitude.
•
Compute the eigenvalue problem including the stresses from the static load. The first eigenvalue corresponds to the value of the critical buckling load.
COMSOL Multiphysics automatically runs the sequence described above and then returns the value of the critical buckling load.
To perform a nonlinear buckling analysis, use the continuation solver to ramp up the load smoothly. You can use a stop condition to automatically stop the solver once a certain criterion is reached. In this example, the stop criterion is the deviation from linearity of the y-displacement in the right arm. The linear displacement response is predicted by using the solution computed under a unit load case for the linear buckling.
Application Library path: Structural_Mechanics_Module/Tutorials/bracket_linear_buckling
Modeling Instructions
Application Libraries
1
From the File menu, choose Application Libraries.
2
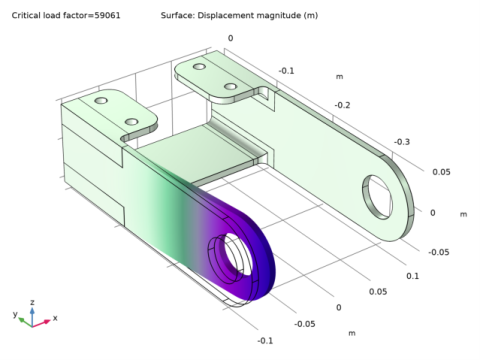
In the Application Libraries window, select Structural Mechanics Module>Tutorials>bracket_basic in the tree.
3
Click  Open.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
F0
1[N]
1 N
Applied force
R
25[mm]
0.025 m
Hole radius
YC
-300[mm]
-0.3 m
Y coordinate of hole center
thick
8[mm]
0.008 m
Bracket arm thickness
P0
2/(thick*pi*R)*F0
3183.1 N/m²
Peak load intensity
Definitions
Analytic 1 (an1)
1
In the Home toolbar, click  Functions and choose Local>Analytic.
2
In the Settings window for Analytic, type load in the Function name text field.
3
Locate the Definition section. In the Expression text field, type F*cos(atan2(py,abs(px))).
4
In the Arguments text field, type F, py, px.
5
Locate the Units section. In the table, enter the following settings:
Argument
Unit
F
Pa
py
m
px
m
6
In the Function text field, type Pa.
Boundary System 1 (sys1)
The load direction does not change with deformation.
1
In the Model Builder window, click Boundary System 1 (sys1).
2
In the Settings window for Boundary System, locate the Settings section.
3
From the Frame list, choose Reference configuration.
Solid Mechanics (solid)
Boundary Load 1
1
In the Model Builder window, under Component 1 (comp1) right-click Solid Mechanics (solid) and choose Boundary Load.
2
In the Settings window for Boundary Load, locate the Boundary Selection section.
3
From the Selection list, choose Right Pin Hole.
4
Locate the Coordinate System Selection section. From the Coordinate system list, choose Boundary System 1 (sys1).
5
Locate the Force section. Specify the FA vector as
0
t1
0
t2
load(-P0,Z,Y-YC)*(Y>YC)
n
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Linear Buckling.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 1
In the Home toolbar, click  Compute.
Results
Mode Shape (solid)
1
Click the  Zoom Extents button in the Graphics toolbar.
The default plot shows the mode shape of the first buckling mode.
Evaluate the y-direction displacement corresponding to the applied unit load.
Point Evaluation 1
1
In the Results toolbar, click  Point Evaluation.
2
In the Settings window for Point Evaluation, locate the Data section.
3
From the Dataset list, choose Study 1/Solution Store 1 (sol2).
4
Select Point 5 only.
5
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
v
m
Displacement field, Y component
6
Click  Evaluate.
You can now evaluate the linear relation between displacement and applied load. This can be used in the later analysis to determine when the nonlinear solution deviates from the linear one.
Definitions
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, locate the Source Selection section.
3
From the Geometric entity level list, choose Point.
4
Select Point 5 only.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Stationary
1
In the Settings window for Stationary, locate the Study Settings section.
2
Select the Include geometric nonlinearity check box.
3
Click to expand the Study Extensions section. Select the Auxiliary sweep check box.
4
Click  Add.
5
In the table, enter the following settings:
Parameter name
Parameter value list
F0 (Applied force)
1 1e3 5e3 1e4 2e4 5.924e4*log10(({range(2,1,10)}+1)/1.1)^(1/5)
Solution 3 (sol3)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 3 (sol3) node.
3
In the Model Builder window, expand the Study 2>Solver Configurations>Solution 3 (sol3)>Stationary Solver 1 node.
4
Right-click Study 2>Solver Configurations>Solution 3 (sol3)>Stationary Solver 1>Parametric 1 and choose Stop Condition.
5
In the Settings window for Stop Condition, locate the Stop Expressions section.
6
Click  Add.
7
In the table, enter the following settings:
Stop expression
Stop if
Active
Description
comp1.intop1(comp1.v)/(F0*1.12E-8)/1.2
True (>=1)
√
Stop expression 1
8
Locate the Output at Stop section. From the Add solution list, choose Step after stop.
9
Clear the Add warning check box.
10
In the Study toolbar, click  Compute.
Results
Stress (solid)
Click the  Zoom Extents button in the Graphics toolbar.
Follow the instructions below to reproduce Figure 2.
1D Plot Group 4
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 2/Solution 3 (sol3).
Point Graph 1
1
Right-click 1D Plot Group 4 and choose Point Graph.
2
Select Point 5 only.
3
In the Settings window for Point Graph, locate the y-Axis Data section.
4
In the Expression text field, type v.
5
From the Unit list, choose mm.
Displacement
1
In the Model Builder window, under Results click 1D Plot Group 4.
2
In the Settings window for 1D Plot Group, type Displacement in the Label text field.
3
Locate the Plot Settings section. Select the x-axis label check box.
4
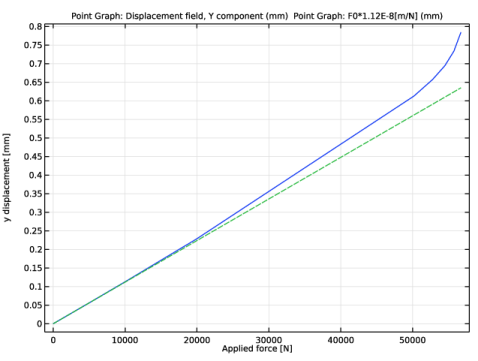
In the associated text field, type Applied force [N].
5
Select the y-axis label check box.
6
In the associated text field, type y displacement [mm].
Point Graph 2
1
Right-click Displacement and choose Point Graph.
2
Select Point 5 only.
3
In the Settings window for Point Graph, locate the y-Axis Data section.
4
In the Expression text field, type F0*1.12E-8[m/N].
5
From the Unit list, choose mm.
6
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
7
In the Displacement toolbar, click  Plot.