
|
|
•
|
|
•
|
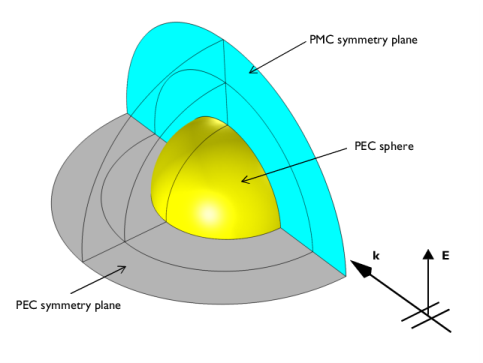
r0 is the unit vector pointing from the origin to the field point p. If the field points lie on a spherical surface S', r0 is the unit normal to S'.
|
|
•
|
n is the unit normal to the surface S.
|
|
•
|
η is the wave impedance:
|
|
•
|
k is the wave number.
|
|
•
|
λ is the wavelength.
|
|
•
|
r is the radius vector (not a unit vector) of the surface S.
|
|
•
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click
|
|
6
|
|
1
|
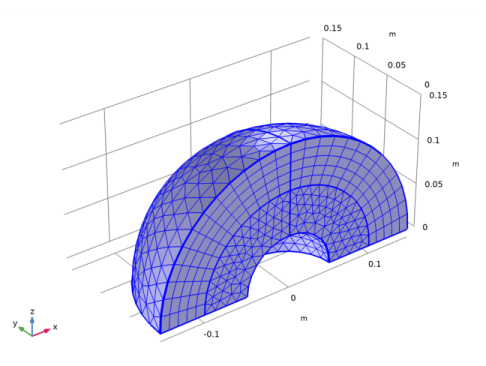
In the Model Builder window, under Component 1 (comp1) right-click Geometry 1 and choose Delete Entities.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (emw).
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
In the Model Builder window, expand the Far-Field Domain 1 node, then click Far-Field Calculation 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
In the tree, select Built-in>Air.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
Locate the Element Size Parameters section. In the Maximum element size text field, type lda/h_size.
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Clear the Description check box.
|
|
7
|
Clear the Type check box.
|
|
8
|
|
9
|
|
10
|
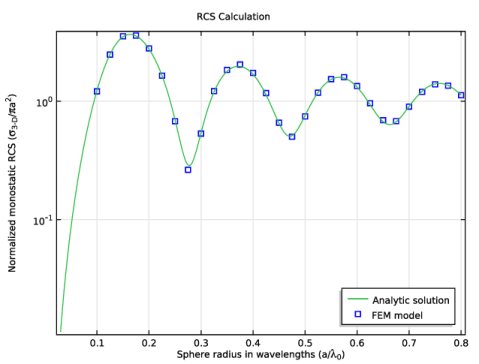
In the associated text field, type Sphere radius in wavelengths (a/\lambda<sub>0</sub>).
|
|
11
|
|
12
|
In the associated text field, type Normalized monostatic RCS (\sigma<sub>3-D</sub>/\pi a<sup>2</sup>).
|
|
13
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose None.
|
|
7
|
|
8
|
|
9
|
|
1
|
|
2
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click OK.
|
|
7
|
|
8
|
Click the Custom button.
|
|
9
|
|
10
|
In the associated text field, type if(lda/h_size>r0/2,r0/2,lda/h_size).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
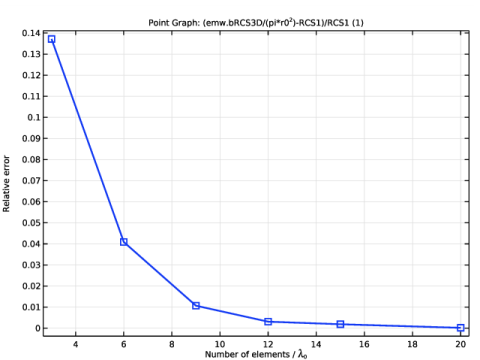
In the associated text field, type Number of elements / \lambda<sub>0</sub>.
|
|
6
|
|
7
|
In the associated text field, type Relative error.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
13
|
|
14
|
|
15
|
|
16
|