PDF
Microstrip Patch Antenna
Introduction
The microstrip patch antenna is used in a wide range of applications because it is easy to design and fabricate. The antenna is attractive due to its low-profile conformal design, relatively low cost, and very narrow bandwidth. This example uses an inset feeding strategy that does not need any additional matching parts.
Figure 1: Microstrip patch antenna. The model consists of a PEC ground plane, a 50 Ω microstrip line fed by a lumped port, a region of free space, and a perfectly matched layer (PML) domain.
Model Definition
Feeding a patch antenna from the edge leads to a very high input impedance, causing an undesirable impedance mismatch if a conventional 50 Ω line is directly connected. One solution to this problem is to use a matching network of quarter-wave transformers between the feed point of the 50 Ω line and the patch. However, this approach has two drawbacks. First, the quarter-wave transformers would be realized as microstrip lines that would have to extend beyond the patch antenna, significantly increasing the overall structure size. Second, these microstrip lines should have a high characteristic impedance and thus would have to be narrower than a possible width for fabrication. Therefore, a better approach is desired.
This example uses a different feed point for the patch antenna to improve matching between the 50 Ω feed and the antenna. It is known that the antenna impedance is higher than 50 Ω if fed from the edge, and lower if fed from the center. Therefore, an optimum feed point exists between the center and the edge. The matching strategy is shown in Figure 2. A 50 Ω microstrip line, fed from the end, extends into the patch antenna structure. The width of the cutout region, W, is chosen to be large enough so that there is minimal coupling between the antenna and the microstrip, but not so large as to significantly affect the antenna characteristics. The length of the microstrip line, L, is chosen to minimize the reflected power, S11. These optimal dimensions can be found via a parametric sweep; this example only treats the final design.
Figure 2: The matching strategy between a 50 Ω line and a patch antenna. A microstrip line of length L extends into a slot of with W cut into the patch antenna.
Results and Discussion
The norm of the electric field inside the antenna substrate is described in Figure 3 where an arrow plot of the electric field is included. The direction of the arrows indicate the dominant polarization in the direction of maximum radiation — the antenna boresight. Figure 4 shows the radiation pattern in the E-plane and H-plane. The E-plane is defined by the direction of the dominant antenna polarization and the H-plane is the plane the magnetic field is mainly polarized in. The 3D far-field radiation pattern is visualized in Figure 5 showing the directive beam pattern due to the ground plane that blocks the radiation toward the bottom side. The calculated antenna directivity is greater than 6.9 dB. With the choice of feed point used in this example, the S11 parameter is better than −10 dB, and the front-to-back ratio in the radiation pattern is more than 15 dB. The frequency response evaluated with 100 kHz resolution is plotted in Figure 7. The −10 dB S11 bandwidth is wider than 10 MHz.
Figure 3: The norm of the electric field is stronger along the radiation edges. The arrow plot shows the dominant direction of polarization of the electric field at the antenna boresight.
Figure 4: Far-field radiation pattern (gain in dBi) at E-plane and H-plane. Because of the bottom ground plane, the radiation pattern is directed toward the top.
Figure 5: The 3D far-field radiation pattern is directed toward the top. The directivity can be evaluated when plotting the 3D far-field pattern.
Figure 6: An isosurface plot visualizes the decay of the field amplitude.
Figure 7: This S-parameter (S11) plot shows that the antenna impedance is matched to 50 Ω around 1.575 GHz.
The 3D full-wave simulation for an antenna array is memory intensive. By using an asymptotic approach such as multiplying the far-field of a single antenna with a uniform array factor, the radiation pattern of an antenna array can be evaluated quickly. Note that this method does not include the coupling among array elements. The 3D uniform array factor function is available under Definitions>Functions from the postprocessing context menu when a Far-Field Calculation feature is defined in the physics interface:
af3(nx, ny, nz, dx, dy, dz, alphax, alphay, alphaz)
where nx, ny, and nz are the number of elements along the x-, y-, and z-axis, respectively. The arguments dx, dy, and dz are the distances between array elements in terms of wavelength. alphax, alphay, and alphaz are the phase progressions in radians. The gain evaluation of a virtual 8-by-8 antenna array in dB scale (Figure 8) uses the following expression:
emw.gaindBEfar+20*log10(emw.af3(8,8,1,0.48,0.48,0,0,0,0))+10*log10(1/64)
Since it is dB scale, the multiplication of the array factor represents a summation in the expression.
 
Table 1: Input arguments of array factor operator for an 8-by-8 Array.
Parameter
Description
Argument
unit
nx
Number of elements along x-axis
8
Dimensionless
ny
Number of elements along y-axis
8
Dimensionless
nz
Number of elements along z-axis
1
Dimensionless
dx
Distance between array elements along x-axis
0.48
Wavelength
dy
Distance between array elements along y-axis
0.48
Wavelength
dz
Distance between array elements along z-axis
0
Wavelength
alphax
Phase progression along x-axis
0
Radian
alphay
Phase progression along y-axis
0
Radian
alphaz
Phase progression along z-axis
0
Radian
It is assumed that the array is excited by a single input uniform distribution network, so the input power needs to be scaled by a factor 10*log10(1/total number of elements). The direction of the main beam can be steered by defining nonzero phase progression in the uniform array factor. The maximum radiation direction of the array factor along the x-axis is defined by the angle θ from the x-axis in the phase progression using
Figure 9 demonstrates the use of the antenna array factor. It includes three plots to show the evolution of the antenna radiation pattern from a single antenna to a synthesized antenna array via the uniform array factor:
1
The gain of the single microstrip patch antenna.
2
The radiation pattern of the uniform array factor configured to have the maximum radiation at 60 degrees from the x-axis by setting the value of alphax as in Table 2.
3
The gain of the 8-by-8 microstrip patch antenna array, using the array factor defined above.
Table 2: Input arguments of array factor operator to steer the beam.
Argument
Value
unit
alphax
-2*pi*0.48*cos(pi/3)
Radian
Figure 8: The far-field radiation pattern of a virtual 8-by-8 microstrip patch antenna array.
Figure 9: The single patch antenna gain, 8-by-8 uniform array factor, 8-by-8 microstrip patch antenna array gain plotted in dB scale.
The final part of this tutorial model demonstrates how mesh adaptation can be used to increase the result accuracy, by making the mesh finer in regions where it matters most for the results. Figure 10 shows the mesh after running the Frequency Domain, RF Adaptive Mesh study. Compared to the initial mesh, the adapted mesh is much finer around the patch edges, except where the field strength is low.
Figure 10: The mesh after running the Frequency Domain, RF Adaptive Mesh study.
Figure 11 shows how the mesh adaptation converges to reach the termination tolerance of 0.02.
Figure 11: This plot shows the convergence of the mesh adaptation process. The process stops when the tolerance of 0.02 is reached.
Finally, Figure 12 shows that the resonance shifts to higher frequencies when using the finer adapted mesh.
Figure 12: A comparison of the frequency spectra for the initial mesh and the adapted mesh.
Notes About the COMSOL Implementation
This example uses the Adaptive Frequency Sweep study step, based on a model order reduction technique, asymptotic waveform evaluation (AWE), to compute the frequency response of the antenna with a fine frequency resolution. This approach is faster than a regular frequency sweep performed in a Frequency Domain study using the same fine frequency resolution, but the analysis is computationally intensive, and it may require more than 5 GB of RAM when running the Adaptive Frequency Sweep. The computed results could be sensitive to the relative tolerance value in the settings window. To enhance the accuracy, a finer value can be applied.
Application Library path: RF_Module/Antenna_Arrays/microstrip_patch_antenna_inset
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  3D.
2
In the Select Physics tree, select Radio Frequency>Electromagnetic Waves, Frequency Domain (emw).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Frequency Domain.
6
Click  Done.
Study 1
Step 1: Frequency Domain
1
In the Model Builder window, under Study 1 click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type 1.575[GHz].
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
d
60[mil]
0.001524 m
Substrate thickness
w_line
3.2[mm]
0.0032 m
50 ohm line width
w_patch
53[mm]
0.053 m
Patch width
l_patch
52[mm]
0.052 m
Patch length
w_stub
7[mm]
0.007 m
Tuning stub width
l_stub
15.5[mm]
0.0155 m
Tuning stub length
w_sub
100[mm]
0.1 m
Substrate width
l_sub
100[mm]
0.1 m
Substrate length
freq_min
1.545[GHz]
1.545E9 Hz
Minimum frequency
freq_max
1.605[GHz]
1.605E9 Hz
Maximum frequency
lda_min
c_const/freq_max
0.18679 m
Minium wavelength
Here mil refers to the unit milliinch, that is 1 mil = 0.0254 mm.
Geometry 1
1
In the Model Builder window, under Component 1 (comp1) click Geometry 1.
2
In the Settings window for Geometry, locate the Units section.
3
From the Length unit list, choose mm.
First, create the substrate block.
Substrate
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, type Substrate in the Label text field.
3
Locate the Size and Shape section. In the Width text field, type w_sub.
4
In the Depth text field, type l_sub.
5
In the Height text field, type d.
6
Locate the Position section. From the Base list, choose Center.
7
Click  Build Selected.
Now add the patch antenna.
Patch
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, type Patch in the Label text field.
3
Locate the Size and Shape section. In the Width text field, type w_patch.
4
In the Depth text field, type l_patch.
5
In the Height text field, type d.
6
Locate the Position section. From the Base list, choose Center.
7
Click  Build Selected.
Create impedance matching parts and a 50Ω feed line.
Stub
1
In the Geometry toolbar, click  Block.
2
In the Settings window for Block, type Stub in the Label text field.
3
Locate the Size and Shape section. In the Width text field, type w_stub.
4
In the Depth text field, type l_stub.
5
In the Height text field, type d.
6
Locate the Position section. From the Base list, choose Center.
7
In the x text field, type w_stub/2+w_line/2.
8
In the y text field, type l_stub/2-l_patch/2.
9
Click  Build Selected.
Copy 1 (copy1)
1
In the Geometry toolbar, click  Transforms and choose Copy.
2
Select the object blk3 only.
3
In the Settings window for Copy, locate the Displacement section.
4
In the x text field, type -w_stub-w_line.
5
Click  Build Selected.
Difference 1 (dif1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the object blk2 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Click to select the  Activate Selection toggle button.
5
Select the objects blk3 and copy1 only.
6
Click  Build Selected.
Choose wireframe rendering to get a better view of the interior parts.
7
Click the  Wireframe Rendering button in the Graphics toolbar.
Continue with the surrounding air and the PML regions.
Sphere 1 (sph1)
1
In the Geometry toolbar, click  Sphere.
2
In the Settings window for Sphere, locate the Size section.
3
In the Radius text field, type l_sub.
4
Click to expand the Layers section. In the table, enter the following settings:
Layer name
Thickness (mm)
Layer 1
l_sub/5
5
Click  Build All Objects.
6
Click the  Zoom Extents button in the Graphics toolbar.
Definitions
Now, add some selections that later will be used when defining selections for materials, physics features, and plots.
Lumped Port
1
In the Definitions toolbar, click  Explicit.
2
In the Settings window for Explicit, type Lumped Port in the Label text field.
3
Locate the Input Entities section. From the Geometric entity level list, choose Boundary.
4
Click  Paste Selection.
5
In the Paste Selection dialog box, type 26 in the Selection text field.
6
Click OK.
Substrate
1
In the Definitions toolbar, click  Explicit.
2
In the Settings window for Explicit, type Substrate in the Label text field.
3
Select Domains 6 and 7 only.
PML
1
In the Definitions toolbar, click  Explicit.
2
In the Settings window for Explicit, type PML in the Label text field.
3
Select Domains 1–4 and 8–11 only.
These are all of the outermost domains of the sphere.
Air
1
In the Definitions toolbar, click  Explicit.
2
In the Settings window for Explicit, type Air in the Label text field.
3
Select Domain 5 only.
PML, Exterior Boundaries
1
In the Definitions toolbar, click  Adjacent.
2
In the Settings window for Adjacent, type PML, Exterior Boundaries in the Label text field.
3
Locate the Input Entities section. Under Input selections, click  Add.
4
In the Add dialog box, select PML in the Input selections list.
5
Click OK.
Air, Exterior Boundaries
1
In the Definitions toolbar, click  Adjacent.
2
In the Settings window for Adjacent, type Air, Exterior Boundaries in the Label text field.
3
Locate the Input Entities section. Under Input selections, click  Add.
4
In the Add dialog box, select Air in the Input selections list.
5
Click OK.
PML, Inside Boundaries
1
In the Definitions toolbar, click  Intersection.
2
In the Settings window for Intersection, type PML, Inside Boundaries in the Label text field.
3
Locate the Geometric Entity Level section. From the Level list, choose Boundary.
4
Locate the Input Entities section. Under Selections to intersect, click  Add.
5
In the Add dialog box, in the Selections to intersect list, choose PML, Exterior Boundaries and Air, Exterior Boundaries.
6
Click OK.
Substrate Boundaries
1
In the Definitions toolbar, click  Adjacent.
2
In the Settings window for Adjacent, type Substrate Boundaries in the Label text field.
3
Locate the Input Entities section. Under Input selections, click  Add.
4
In the Add dialog box, select Substrate in the Input selections list.
5
Click OK.
Perfectly Matched Layer 1 (pml1)
1
In the Definitions toolbar, click  Perfectly Matched Layer.
2
In the Settings window for Perfectly Matched Layer, locate the Domain Selection section.
3
From the Selection list, choose PML.
4
Locate the Geometry section. From the Type list, choose Spherical.
View 1
Suppress some domains and boundaries. This helps to see the interior parts when setting up the physics and reviewing the mesh.
Hide for Physics 1
1
In the Model Builder window, right-click View 1 and choose Hide for Physics.
2
Select Domains 2 and 9 only.
Hide for Physics 2
1
Right-click View 1 and choose Hide for Physics.
2
In the Settings window for Hide for Physics, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundaries 10 and 33 only.
Hidden domains and boundaries can be shown by pressing the View All, View Hidden Only, or Reset Hiding button in the Graphic Window toolbar.
Before creating the materials for the model, specify the physics. Using this information, the software can detect which material properties are needed.
Electromagnetic Waves, Frequency Domain (emw)
Perfect Electric Conductor 2
1
In the Model Builder window, under Component 1 (comp1) right-click Electromagnetic Waves, Frequency Domain (emw) and choose Perfect Electric Conductor.
2
Select Boundaries 15, 20, and 21 only.
Lumped Port 1
1
In the Physics toolbar, click  Boundaries and choose Lumped Port.
2
In the Settings window for Lumped Port, locate the Boundary Selection section.
3
From the Selection list, choose Lumped Port.
4
Click the  Zoom In button in the Graphics toolbar.
For the first port, wave excitation is on by default.
Far-Field Domain 1
In the Physics toolbar, click  Domains and choose Far-Field Domain.
Add Material
1
In the Home toolbar, click  Add Material to open the Add Material window.
2
Go to the Add Material window.
3
In the tree, select Built-in>Air.
4
Click Add to Component in the window toolbar.
5
In the Home toolbar, click  Add Material to close the Add Material window.
Materials
Substrate
1
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
2
In the Settings window for Material, type Substrate in the Label text field.
3
Locate the Geometric Entity Selection section. From the Selection list, choose Substrate.
4
Locate the Material Contents section. In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Relative permittivity
epsilonr_iso ; epsilonrii = epsilonr_iso, epsilonrij = 0
3.38
1
Basic
Relative permeability
mur_iso ; murii = mur_iso, murij = 0
1
1
Basic
Electrical conductivity
sigma_iso ; sigmaii = sigma_iso, sigmaij = 0
0
S/m
Basic
Mesh 1
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Build All.
Study 1
In the Home toolbar, click  Compute.
Results
Multislice
1
In the Model Builder window, expand the Results>Electric Field (emw) node, then click Multislice.
2
In the Settings window for Multislice, locate the Multiplane Data section.
3
Find the X-planes subsection. In the Planes text field, type 0.
4
Find the Y-planes subsection. In the Planes text field, type 0.
5
Locate the Coloring and Style section. From the Color table list, choose ThermalDark.
Selection 1
1
Right-click Multislice and choose Selection.
2
Select Domains 6 and 7 only.
Electric Field (emw)
1
In the Model Builder window, under Results click Electric Field (emw).
2
In the Settings window for 3D Plot Group, locate the Plot Settings section.
3
Clear the Plot dataset edges check box.
Arrow Volume 1
1
Right-click Electric Field (emw) and choose Arrow Volume.
2
In the Electric Field (emw) toolbar, click  Plot.
3
In the Model Builder window, click Arrow Volume 1.
4
In the Settings window for Arrow Volume, locate the Arrow Positioning section.
5
Find the X grid points subsection. In the Points text field, type 1.
6
Find the Y grid points subsection. In the Points text field, type 31.
7
Find the Z grid points subsection. In the Points text field, type 31.
8
Locate the Coloring and Style section. From the Arrow length list, choose Logarithmic.
Selection 1
1
Right-click Arrow Volume 1 and choose Selection.
2
Select Domain 5 only.
Color Expression 1
1
In the Model Builder window, right-click Arrow Volume 1 and choose Color Expression.
2
In the Settings window for Color Expression, locate the Expression section.
3
In the Expression text field, type 20*log10(emw.normE).
4
In the Electric Field (emw) toolbar, click  Plot.
Strong electric fields are observed on the radiating edges. See Figure 3 and check the dominant polarization at the boresight.
2D Far Field (emw)
1
In the Model Builder window, under Results click 2D Far Field (emw).
2
In the Settings window for Polar Plot Group, click to expand the Title section.
3
From the Title type list, choose Manual.
4
In the Title text area, type Far-field gain, dBi.
Radiation Pattern 1
1
In the Model Builder window, expand the 2D Far Field (emw) node, then click Radiation Pattern 1.
2
In the Settings window for Radiation Pattern, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Far field>emw.gaindBEfar - Far-field gain, dBi.
3
Locate the Evaluation section. Find the Reference direction subsection. In the x text field, type 0.
4
In the y text field, type 1.
5
Find the Normal vector subsection. In the x text field, type 1.
6
In the z text field, type 0.
7
Click to expand the Legends section. From the Legends list, choose Manual.
8
In the table, enter the following settings:
Legends
E-plane
Radiation Pattern 2
1
Right-click Results>2D Far Field (emw)>Radiation Pattern 1 and choose Duplicate.
2
In the Settings window for Radiation Pattern, locate the Evaluation section.
3
Find the Normal vector subsection. In the x text field, type 0.
4
In the y text field, type -1.
5
Find the Reference direction subsection. In the x text field, type 1.
6
In the y text field, type 0.
7
Click to expand the Coloring and Style section. Find the Line style subsection. From the Line list, choose Dashed.
8
Locate the Legends section. In the table, enter the following settings:
Legends
H-plane
9
In the 2D Far Field (emw) toolbar, click  Plot.
This is the far-field gain patterns on the E- and H-plane (Figure 4). The E- and H-plane of a linearly polarized antenna are defined by the dominant polarization at the boresight. The E-plane includes the main polarization, Ey in this model, while the H-plane is perpendicular to the main polarization.
Radiation Pattern 1
The default 3D far-field plot evaluates the norm of the electric far field that is calculated from the near field using the Stratton-Chu formula. When the 3D far-field is visualized and Compute directivity is on, it also calculates the maximum directivity of an antenna. The default Directivity expression for Electromagnetic Waves, Frequency Domain is set to emw.normEfar^2, since antenna directivity is defined by the maximum radiation intensity, that is, the maximum power density per unit solid angle. The directivity calculation is used not only for electromagnetics but also for other physics such as acoustics, where the Directivity expression has a different input expression. The calculated maximum directivity value for the microstrip patch antenna is around 6.9 dB.
Annotation 1
1
In the Model Builder window, expand the Results>3D Far Field, Gain (emw) node.
2
Right-click 3D Far Field, Gain (emw) and choose Annotation.
3
In the Settings window for Annotation, locate the Annotation section.
4
In the Text text field, type Maximum directivity: 6.9 dB.
5
Locate the Position section. In the Z text field, type 1.71.
The location is set based on the maximum value of normEfar at the antenna boresight.
6
Locate the Coloring and Style section. From the Background color list, choose White.
7
Select the Show frame check box.
8
In the 3D Far Field, Gain (emw) toolbar, click  Plot.
Compare the 3D far-field radiation pattern plot with Figure 5.
Inspect the input matching property (S11) at the simulated frequency.
3D Plot Group 4
1
In the Model Builder window, expand the Results>Derived Values node.
2
Right-click Results and choose 3D Plot Group.
Isosurface 1
1
In the Model Builder window, right-click 3D Plot Group 4 and choose Isosurface.
2
In the Settings window for Isosurface, locate the Expression section.
3
In the Expression text field, type 20*log10(emw.normE).
4
Locate the Levels section. In the Total levels text field, type 20.
Selection 1
1
Right-click Isosurface 1 and choose Selection.
2
Select Domains 5–7 only.
Filter 1
1
In the Model Builder window, right-click Isosurface 1 and choose Filter.
2
In the Settings window for Filter, locate the Element Selection section.
3
In the Logical expression for inclusion text field, type x>0.
4
In the 3D Plot Group 4 toolbar, click  Plot.
Figure 6 shows the above isosurface plot.
Note that the following simulation requires more than 5 GB RAM.
In order to have the S-parameter plot of the microstrip patch antenna with a fine frequency resolution, analyze the model using Adaptive Frequency Sweep based on asymptotic waveform evaluation (AWE). When a device presents a slowly varying frequency response, the AWE solver is much faster than the regular frequency domain solver, when running the simulation for many frequency points.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Adaptive Frequency Sweep.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
Step 1: Adaptive Frequency Sweep
1
In the Model Builder window, under Study 2 click Step 1: Adaptive Frequency Sweep.
2
In the Settings window for Adaptive Frequency Sweep, locate the Study Settings section.
3
In the Frequencies text field, type range(freq_min,100[kHz],freq_max).
A slowly varying scalar value curve works well for AWE expressions. For one-port devices like antennas, a trivial AWE expression is S11. However, if the frequency response of the AWE expression contains an infinite gradient — the case for the S11 value of an antenna, with excellent impedance matching at a single frequency point — the simulation will take longer to complete. If the loss from the antenna is negligible, an alternative expression such as sqrt(1-abs(comp1.emw.S11)^2) may work well and reduce the computation time. When AWE expression type is set to Physics controlled in the Adaptive Frequency Sweep study settings, sqrt(1-abs(comp1.emw.S11)^2) is used automatically for one-port devices.
Because such a fine frequency step generates a memory-intensive solution, the model file size will increase tremendously when it is saved. When only the frequency response of port related variables is of interest, it is not necessary to store all of the field solutions. By selecting the Store fields in output check box in the Values of Dependent Variables section, we can control the part of the model on which the computed solution is saved. We only add the selection containing the boundaries where the port variables are calculated. The lumped port size is typically very small compared to the entire modeling domain, and the saved file size with the fine frequency step is more or less that of the regular discrete frequency sweep model when only the solutions on the lumped port boundaries are stored.
4
Locate the Values of Dependent Variables section. Find the Store fields in output subsection. From the Settings list, choose For selections.
5
Under Selections, click  Add.
6
In the Add dialog box, select Lumped Port in the Selections list.
7
Click OK.
It is necessary to include the lumped port boundaries to calculate the S-parameters. By choosing only the lumped port boundaries for Store fields in output settings, it is possible to significantly reduce the size of the model file.
8
In the Home toolbar, click  Compute.
Results
S-parameter, Asymptotic Waveform Evaluation
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type S-parameter, Asymptotic Waveform Evaluation in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 2/Solution 2 (sol2).
4
Click to expand the Title section. From the Title type list, choose Manual.
5
In the Title text area, type Adaptive Frequency Sweep, Microstrip Patch Antenna.
6
Locate the Legend section. From the Position list, choose Lower right.
Global 1
1
Right-click S-parameter, Asymptotic Waveform Evaluation and choose Global.
2
In the Settings window for Global, click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>emw.S11dB - S11.
3
In the S-parameter, Asymptotic Waveform Evaluation toolbar, click  Plot.
Review the S-parameter plot in Figure 7.
The following instructions show how to perform a quick evaluation of the far-field radiation pattern of an antenna array using the uniform array factor operator.
3D Far Field, Virtual Array
1
In the Home toolbar, click  Add Plot Group and choose 3D Plot Group.
2
In the Settings window for 3D Plot Group, type 3D Far Field, Virtual Array in the Label text field.
3
Locate the Color Legend section. Select the Show maximum and minimum values check box.
Radiation Pattern 1
1
In the 3D Far Field, Virtual Array toolbar, click  More Plots and choose Radiation Pattern.
2
In the Settings window for Radiation Pattern, locate the Expression section.
3
In the Expression text field, type emw.gaindBEfar+20*log10(emw.af3(8,8,1,0.48,0.48,0,0,0,0))+10*log10(1/64).
See the Results and Discussion section for the usage of the uniform array factor operator af3.
4
Select the Threshold check box.
5
In the associated text field, type -30.
6
Locate the Evaluation section. Find the Angles subsection. In the Number of elevation angles text field, type 180.
7
In the Number of azimuth angles text field, type 180.
8
Locate the Coloring and Style section. From the Color table list, choose HeatCamera.
9
In the 3D Far Field, Virtual Array toolbar, click  Plot.
The far-field radiation pattern of a virtual 8x8 microstrip patch antenna array is plotted in Figure 8.
2D Far Field Gain (dB), Virtual Array
1
In the Home toolbar, click  Add Plot Group and choose Polar Plot Group.
2
In the Settings window for Polar Plot Group, type 2D Far Field Gain (dB), Virtual Array in the Label text field.
3
Locate the Title section. From the Title type list, choose Manual.
4
In the Title text area, type 8x8 Microstrip Patch Antenna Array.
5
Locate the Axis section. Select the Manual axis limits check box.
6
In the r minimum text field, type -15.
7
In the r maximum text field, type 25.
8
Locate the Legend section. From the Position list, choose Upper left.
Radiation Pattern 1
1
In the 2D Far Field Gain (dB), Virtual Array toolbar, click  More Plots and choose Radiation Pattern.
2
In the Settings window for Radiation Pattern, locate the Expression section.
3
In the Expression text field, type emw.gaindBEfar.
4
Locate the Evaluation section. Find the Angles subsection. In the Number of angles text field, type 360.
5
Find the Normal vector subsection. In the y text field, type -1.
6
In the z text field, type 0.
7
Locate the Legends section. Select the Show legends check box.
8
From the Legends list, choose Manual.
9
In the table, enter the following settings:
Legends
Single patch antenna gain
10
In the 2D Far Field Gain (dB), Virtual Array toolbar, click  Plot.
Radiation Pattern 2
1
Right-click Radiation Pattern 1 and choose Duplicate.
2
In the Settings window for Radiation Pattern, locate the Expression section.
3
In the Expression text field, type 20*log10(emw.af3(8,8,1,0.48,0.48,0,-2*pi*0.48*cos(pi/3),0,0))+10*log10(1/64).
4
Locate the Legends section. In the table, enter the following settings:
Legends
8x8 uniform array factor
5
In the 2D Far Field Gain (dB), Virtual Array toolbar, click  Plot.
Radiation Pattern 3
1
Right-click Radiation Pattern 2 and choose Duplicate.
2
In the Settings window for Radiation Pattern, locate the Expression section.
3
In the Expression text field, type emw.gaindBEfar+20*log10(emw.af3(8,8,1,0.48,0.48,0,-2*pi*0.48*cos(pi/3),0,0))+10*log10(1/64).
4
Locate the Legends section. In the table, enter the following settings:
Legends
8x8 patch antenna array gain
5
In the 2D Far Field Gain (dB), Virtual Array toolbar, click  Plot.
See Figure 9 for the dB-scaled gain of the virtual 8x8 microstrip patch antenna array. It is plotted with the uniform array factor which has the maximum radiation at 60 degrees from the x-axis.
Geometry 1
Next, perform a Frequency Domain, RF Adaptive Mesh study. To improve the mesh adaptation process, the thickness of the PML should be of the same order as the wavelength. Thus, start by changing the thickness of the sphere layer that represents the PML.
Sphere 1 (sph1)
1
In the Model Builder window, under Component 1 (comp1)>Geometry 1 click Sphere 1 (sph1).
2
In the Settings window for Sphere, locate the Size section.
3
In the Radius text field, type l_sub+lda_min.
4
Locate the Layers section. In the table, enter the following settings:
Layer name
Thickness (mm)
Layer 1
lda_min
5
Click  Build All Objects.
6
Click the  Zoom Extents button in the Graphics toolbar.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Frequency Domain, RF Adaptive Mesh.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 3
Step 1: Frequency Domain, RF Adaptive Mesh
1
In the Settings window for Frequency Domain, RF Adaptive Mesh, locate the Study Settings section.
2
Click  Range.
3
In the Range dialog box, choose Number of values from the Entry method list.
4
In the Start text field, type freq_min.
5
In the Stop text field, type freq_max.
6
In the Number of values text field, type 5.
7
Click Replace.
8
In the Model Builder window, click Study 3.
9
In the Settings window for Study, locate the Study Settings section.
10
Clear the Generate default plots check box, as the default S-parameter and far-field plots are not of interest for the mesh adaptation study. However, in the following steps a field plot is built, so the mesh adaptation progress can be followed while solving.
Solution 3 (sol3)
In the Study toolbar, click  Show Default Solver, to create the dataset for this study. The field plot that will be created will refer to this dataset.
Results
Electric Field (emw), Mesh Adaptation
1
In the Home toolbar, click  Add Plot Group and choose 3D Plot Group.
2
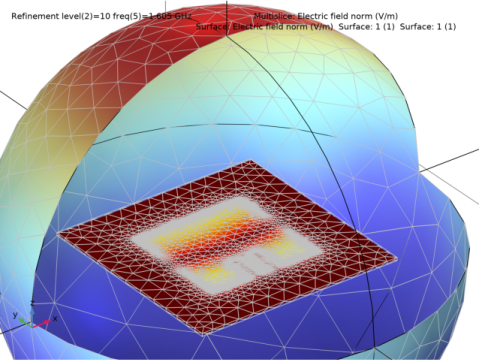
In the Settings window for 3D Plot Group, type Electric Field (emw), Mesh Adaptation in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 3/Adaptive Mesh Refinement Solutions 1 (sol4).
Multislice 1
1
In the Electric Field (emw), Mesh Adaptation toolbar, click  More Plots and choose Multislice.
2
In the Settings window for Multislice, locate the Multiplane Data section.
3
Find the X-planes subsection. In the Planes text field, type 0.
4
Find the Y-planes subsection. In the Planes text field, type 0.
5
Locate the Coloring and Style section. From the Color table list, choose Thermal.
Selection 1
1
Right-click Multislice 1 and choose Selection.
2
In the Settings window for Selection, locate the Selection section.
3
From the Selection list, choose Substrate.
Electric Field (emw), Mesh Adaptation
1
In the Model Builder window, under Results click Electric Field (emw), Mesh Adaptation.
2
In the Settings window for 3D Plot Group, locate the Color Legend section.
3
Clear the Show legends check box.
Surface 1
1
Right-click Electric Field (emw), Mesh Adaptation and choose Surface.
2
In the Settings window for Surface, locate the Coloring and Style section.
3
From the Color table list, choose RainbowLight.
Selection 1
1
Right-click Surface 1 and choose Selection.
2
In the Settings window for Selection, locate the Selection section.
3
From the Selection list, choose PML, Inside Boundaries.
4
In the list, choose 10 (hidden) and 33 (hidden).
5
Click  Remove from Selection, to avoid that the mesh is visualized on the boundaries that otherwise are hidden in the physics view.
6
Select Boundaries 9, 11, 12, 32, 37, and 40 only.
Surface 2
1
In the Model Builder window, under Results>Electric Field (emw), Mesh Adaptation right-click Surface 1 and choose Duplicate, to add the first of two surface plots to visualize the mesh.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type 1.
4
Locate the Coloring and Style section. From the Coloring list, choose Uniform.
5
From the Color list, choose Gray.
6
Select the Wireframe check box.
Surface 3
Right-click Surface 2 and choose Duplicate.
Selection 1
1
In the Model Builder window, expand the Surface 3 node, then click Selection 1.
2
In the Settings window for Selection, locate the Selection section.
3
From the Selection list, choose Substrate Boundaries.
Study 3
Step 1: Frequency Domain, RF Adaptive Mesh
1
In the Model Builder window, under Study 3 click Step 1: Frequency Domain, RF Adaptive Mesh.
2
In the Settings window for Frequency Domain, RF Adaptive Mesh, locate the Study Settings section.
3
In the Damping factor text field, type 0.05.
4
In the Maximum number of adaptations text field, type 20.
5
Click to expand the Results While Solving section. Select the Plot check box.
6
From the Plot group list, choose Electric Field (emw), Mesh Adaptation.
Adjust the view, to clearly see the mesh on both the substrate and the boundary towards the PML.
7
Click the  Zoom Extents button in the Graphics toolbar.
8
Click the  Zoom In button in the Graphics toolbar.
9
Click the  Zoom In button in the Graphics toolbar.
10
Click the  Zoom In button in the Graphics toolbar.
11
In the Home toolbar, click  Compute.
In the Graphics window, follow how the mesh is adapted while solving.
Results
Electric Field (emw), Mesh Adaptation
Notice that the mesh is much denser in the adapted mesh around the patch edges, compared to the original mesh, except where the field strength is low.
Goal-oriented termination expression 1D Plot Group 9
This plot shows how the mesh adaptation converges and stops when the increment size is less than the tolerance of 0.02.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Adaptive Frequency Sweep.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 4
1
In the Model Builder window, click Study 4.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box, as we again will not be saving the field in this study. Thereby, it doesn’t make sense generating the default field plots.
Step 1: Adaptive Frequency Sweep
1
In the Model Builder window, under Study 4 click Step 1: Adaptive Frequency Sweep.
2
In the Settings window for Adaptive Frequency Sweep, locate the Study Settings section.
3
In the Frequencies text field, type range(freq_min,100[kHz],freq_max).
4
Locate the Values of Dependent Variables section. Find the Store fields in output subsection. From the Settings list, choose For selections.
5
Under Selections, click  Add.
6
In the Add dialog box, select Lumped Port in the Selections list.
7
Click OK.
Again, only include the lumped port boundaries to calculate S-parameters, to reduce the size of the model.
8
In the Home toolbar, click  Compute.
Results
S-parameter, Asymptotic Waveform Evaluation on Adaptive Mesh
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type S-parameter, Asymptotic Waveform Evaluation on Adaptive Mesh in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 4/Solution 16 (sol16).
4
Locate the Title section. From the Title type list, choose Manual.
5
In the Title text area, type Adaptive Frequency Sweep, Microstrip Patch Antenna.
6
Locate the Legend section. From the Position list, choose Lower left.
Global 1
1
Right-click S-parameter, Asymptotic Waveform Evaluation on Adaptive Mesh and choose Global.
2
In the Settings window for Global, click Add Expression in the upper-right corner of the y-Axis Data section. From the menu, choose Component 1 (comp1)>Electromagnetic Waves, Frequency Domain>Ports>emw.S11dB - S11.
3
Click to expand the Legends section. From the Legends list, choose Manual.
4
In the table, enter the following settings:
Legends
Adaptive Mesh
5
Right-click Global 1 and choose Copy.
Global 2
1
In the Model Builder window, right-click S-parameter, Asymptotic Waveform Evaluation on Adaptive Mesh and choose Paste Global.
2
In the Settings window for Global, locate the Data section.
3
From the Dataset list, choose Study 2/Solution 2 (sol2).
4
Locate the Legends section. In the table, enter the following settings:
Legends
Initial Mesh
5
In the S-parameter, Asymptotic Waveform Evaluation on Adaptive Mesh toolbar, click  Plot.
For the denser, adapted mesh, the resonance has shifted to a slightly higher frequency.