
|
|
•
|
|
•
|
|
•
|
|
•
|
V (SI unit: V) is the electric potential,
|
|
•
|
N (dimensionless) is the total number of particles,
|
|
•
|
r (SI unit: m) is the position vector,
|
|
•
|
|
•
|
δ (SI unit: 1/m3) is the Dirac delta function.
|
|
1
|
Compute the particle trajectories in the time domain, ignoring Coulomb forces. Compute the space charge density using the Electric Particle Field Interaction node.
|
|
1
|
|
2
|
In the Select Physics tree, select AC/DC>Particle Tracing>Particle Field Interaction, Non-Relativistic.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Charged Particle Tracing>Bidirectionally Coupled Particle Tracing.
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file electron_beam_divergence_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
On the object cyl1, select Boundary 3 only.
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Charged Particle Tracing (cpt) click Particle Properties 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
3
|
|
4
|
|
5
|
Locate the Advanced Settings section. Select the Use piecewise polynomial recovery on field check box.
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Bidirectionally Coupled Particle Tracing, locate the Study Settings section.
|
|
3
|
Click
|
|
4
|
|
5
|
|
6
|
Click Replace.
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
13
|
|
1
|
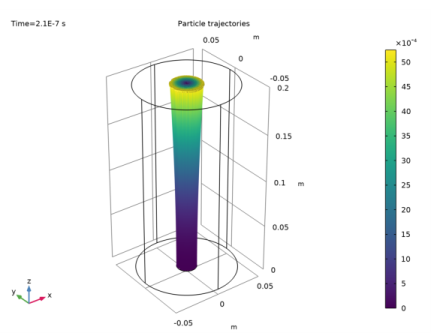
In the Model Builder window, expand the Results>Particle Trajectories (cpt) node, then click Particle Trajectories 1.
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Particle Trajectories 1 node, then click Color Expression 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
Click
|