PDF
Elastoplastic Analysis of Holed Plate
Introduction
In this example you analyze a perforated plate loaded into the plastic regime. In addition to the original problem, which you can find in section 7.10 of The Finite Element Method by O.C. Zienkiewicz (Ref. 1), you can also study the unloading of the plate.
The model also shows how to apply an external hardening function based on an interpolated stress-strain curve.
Model Definition
Figure 1 shows the plate’s geometry. Due to the double symmetry of the geometry you only need to analyze a quarter of the plate.
Figure 1: The plate geometry.
Because the plate is thin and the loads are in plane, you can assume a plane stress condition.
Material
•
Elastic properties: E = 70000 MPa and ν = 0.2.
•
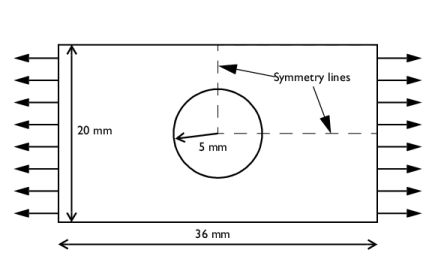
Plastic properties: Yield stress 243 MPa and a linear isotropic hardening with tangent modulus 2171 MPa.
Constraints and loads
•
Symmetry plane constraints are applied on the leftmost vertical boundary and the lower horizontal boundary.
•
The right vertical edge is subjected to a stress, which increases from zero to a maximum value of 133.65 MPa and then is released again. The peak value is selected so that the mean stress over the section through the hole is 10% above the yield stress (=1.1·243·(20−10)/20).
Results and Discussion
Figure 2 shows the development of the plastic region. The parameter values are 0.55, 0.65, 0.75, 0.85, 0.95, and 1.05. These values are proportional to the load with a parameter value 1.0, which corresponds to the yield limit of the average stress over the cross section through the hole. For a material without strain hardening, the structure would thus have collapsed before reaching the final load level. Because an elastoplastic solution is load-path dependent, it is important not to use too large steps in the load parameter when you anticipate a plastic flow. Usually you can take one large step up to the elastic limit, as this example shows. Moreover, reversed plastic flow can occur during the unloading. This is why this study uses small parameter steps at the end of the parameter range.
Figure 2: Development of plastic region (red) for parameter values 0.55, 0.65, 0.75, 0.85, 0.95 and 1.05.
Modeling with COMSOL Multiphysics
In this example there are two studies where the only difference is how the hardening data of the plasticity model is entered. In the first study, you give the data in the most natural way, since a linear hardening can be entered directly using the tangent modulus.
In the second study, it is shown how to proceed when you have a tabulated data from a general tensile test. Note that in metal plasticity, the hardening function σh to be entered is the stress added to the initial yield stress σys0 as function of the equivalent plastic strain εpe. Thus, the function must always pass the point (0,0). If your tabulated data contains total stress versus total strain, the hardening function must thus be written as
where, σe is the equivalent (von Mises) stress, E is the Young’s modulus, and σtab is an interpolation function of your tabulated data. Figure 4 shows the linear elastic and plastic regions.
Figure 3: The interpolated stress-strain curve shows both the elastic and hardening regions.
The results show in Figure 4 and Figure 5 are in good agreement. In Study 1, isotropic hardening is generated with an isotropic tangent modulus ETiso = 2.171 GPa, and in Study 2 it is generated with interpolated hardening function data, which mimics the isotropic tangent modulus from Study 1.
Figure 4: Deformation and von Mises stress for parameter value 2.2. The hardening was implemented with isotropic tangent modulus ETiso = 2.171 GPa.
Figure 5: Deformation and von Mises stress for parameter value 2.2. The hardening was implemented with the interpolated hardening function.
Reference
1. O.C. Zienkiewicz and R.L. Taylor, The Finite Element Method, 4th ed., McGraw-Hill, 1991.
Application Library path: Nonlinear_Structural_Materials_Module/Plasticity/elastoplastic_plate
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D.
2
In the Select Physics tree, select Structural Mechanics>Solid Mechanics (solid).
3
Click Add.
4
Click  Study.
5
In the Select Study tree, select General Studies>Stationary.
6
Click  Done.
Geometry 1
Begin by changing the length unit to millimeters.
1
In the Model Builder window, under Component 1 (comp1) click Geometry 1.
2
In the Settings window for Geometry, locate the Units section.
3
From the Length unit list, choose mm.
Rectangle 1 (r1)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 18.
4
In the Height text field, type 10.
5
Click  Build Selected.
Circle 1 (c1)
1
In the Geometry toolbar, click  Circle.
2
In the Settings window for Circle, locate the Size and Shape section.
3
In the Radius text field, type 5.
4
Click  Build Selected.
Difference 1 (dif1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Difference.
2
Select the object r1 only.
3
In the Settings window for Difference, locate the Difference section.
4
Find the Objects to subtract subsection. Click to select the  Activate Selection toggle button.
5
Select the object c1 only.
6
Click  Build Selected.
Add a solver parameter for controlling the load expression.
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
In the table, enter the following settings:
Name
Expression
Value
Description
para
0
0
Horizontal load parameter
Definitions
Interpolation 1 (int1)
1
In the Home toolbar, click  Functions and choose Local>Interpolation.
2
In the Settings window for Interpolation, locate the Definition section.
3
In the Function name text field, type loadfunc.
4
In the table, enter the following settings:
t
f(t)
0
0
1.1
133.65
2.2
0
5
Locate the Units section. In the Argument table, enter the following settings:
Argument
Unit
t
1
6
In the Function table, enter the following settings:
Function
Unit
loadfunc
MPa
7
Click  Plot.
The interpolation function defines the load function.
Solid Mechanics (solid)
1
In the Model Builder window, under Component 1 (comp1) click Solid Mechanics (solid).
2
In the Settings window for Solid Mechanics, locate the 2D Approximation section.
3
From the list, choose Plane stress.
4
Locate the Thickness section. In the d text field, type 10[mm].
Linear Elastic Material 1
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Linear Elastic Material 1.
Linear Hardening
1
In the Physics toolbar, click  Attributes and choose Plasticity.
2
In the Settings window for Plasticity, type Linear Hardening in the Label text field.
Materials
Material 1 (mat1)
1
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Young’s modulus
E
70e9
Pa
Young’s modulus and Poisson’s ratio
Poisson’s ratio
nu
0.2
1
Young’s modulus and Poisson’s ratio
Density
rho
7850
kg/m³
Basic
Initial yield stress
sigmags
243e6
Pa
Elastoplastic material model
Isotropic tangent modulus
Et
2.171e9
Pa
Elastoplastic material model
Solid Mechanics (solid)
Symmetry 1
1
In the Physics toolbar, click  Boundaries and choose Symmetry.
2
Select Boundaries 1 and 3 only.
Boundary Load 1
1
In the Physics toolbar, click  Boundaries and choose Boundary Load.
2
Select Boundary 4 only.
3
In the Settings window for Boundary Load, locate the Force section.
4
Specify the FA vector as
loadfunc(para)
x
0
y
Mesh 1
Free Triangular 1
1
In the Mesh toolbar, click  Free Triangular.
The mesh should be refined in areas of anticipated high stress and strain gradients.
Refine 1
1
In the Mesh toolbar, click  Modify and choose Refine.
2
In the Settings window for Refine, click to expand the Refine Elements in Box section.
3
Select the Specify bounding box check box.
4
In row x, set Upper bound to 8.
5
In row y, set Upper bound to 10.
6
In the Model Builder window, right-click Mesh 1 and choose Build All.
The mesh should consist of around 700 elements.
Study 1
Step 1: Stationary
Set up an auxiliary continuation sweep for the para parameter.
1
In the Model Builder window, under Study 1 click Step 1: Stationary.
2
In the Settings window for Stationary, click to expand the Study Extensions section.
3
Select the Auxiliary sweep check box.
4
Click  Add.
5
In the table, enter the following settings:
Parameter name
Parameter value list
para (Horizontal load parameter)
0 range(0.40,0.05,2.2)
With these settings, the edge load you defined earlier increases from zero to a maximum value of 133.65 MPa and is then released.
6
In the Model Builder window, click Study 1.
7
In the Settings window for Study, type Linear Hardening in the Label text field.
8
In the Home toolbar, click  Compute.
Results
The first default plot shows the von Mises stress for the final parameter value.
Stress, Linear Hardening
1
In the Model Builder window, under Results click Stress (solid).
2
In the Settings window for 2D Plot Group, type Stress, Linear Hardening in the Label text field.
Visualize the plastic zone using a Boolean expression solid.epeGp>0 which is 1 in the plastic region and 0 elsewhere.
Plastic Region, Linear Hardening
1
In the Model Builder window, under Results click Equivalent Plastic Strain (solid).
2
In the Settings window for 2D Plot Group, type Plastic Region, Linear Hardening in the Label text field.
Contour 1
1
In the Model Builder window, expand the Plastic Region, Linear Hardening node, then click Contour 1.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type solid.epeGp>0.
Plastic Region, Linear Hardening
1
In the Model Builder window, click Plastic Region, Linear Hardening.
2
In the Settings window for 2D Plot Group, locate the Data section.
3
From the Parameter value (para) list, choose 0.55.
4
In the Plastic Region, Linear Hardening toolbar, click  Plot.
The plot in the Graphics window should now look like that in the upper-left panel of Figure 2.
5
Repeat steps 3, 4 and 5 for Parameter value (para) 0.65, 0.75, 0.85, 0.95, and 1.05 to reproduce the remaining subplots in Figure 2.
Hardening with Experimental Stress-Strain Curve and user defined yield function.
To fit the first study case, the stress-strain curve will be very simple, an elastic slope of 70 GPa and then a plastic slope of 2.171 GPa. Only three points are needed to define the stress-strain curve in this simple case.
Definitions
Interpolation 2 (int2)
1
In the Home toolbar, click  Functions and choose Local>Interpolation.
2
In the Settings window for Interpolation, locate the Definition section.
3
In the Function name text field, type stress_strain_curve.
4
In the table, enter the following settings:
t
f(t)
0
0
243e6/70e9
243e6
243e6/70e9+50e6/2.171e9
243e6+50e6
5
Locate the Units section. In the Argument table, enter the following settings:
Argument
Unit
t
1
6
In the Function table, enter the following settings:
Function
Unit
stress_strain_curve
Pa
7
Locate the Interpolation and Extrapolation section. From the Extrapolation list, choose Linear.
8
Click  Plot.
Add a variable for controlling the hardening.
Variables 1
1
In the Home toolbar, click  Variables and choose Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Unit
Description
hardening
max(0,stress_strain_curve(solid.epe+solid.mises/solid.E)-solid.sigmags)
Pa
Hardening function
Solid Mechanics (solid)
Linear Elastic Material 1
In the Model Builder window, under Component 1 (comp1)>Solid Mechanics (solid) click Linear Elastic Material 1.
Interpolated Hardening and User Defined Plastic Flow
1
In the Physics toolbar, click  Attributes and choose Plasticity.
2
In the Settings window for Plasticity, type Interpolated Hardening and User Defined Plastic Flow in the Label text field.
Define the von Mises stress in terms of the second invariant of the stress tensor.
3
Locate the Plasticity Model section. From the Yield function F list, choose User defined.
4
In the φ(σ) text field, type sqrt(3*solid.II2sEff).
Add a small value to the potential to avoid possible division of zero when evaluating its derivative at zero stress.
5
From the Plastic potential Q list, choose User defined.
6
In the Q text field, type sqrt(3*solid.II2sEff+eps).
Use hardening function data and add the hardening function to the material properties.
7
Find the Isotropic hardening model subsection. From the list, choose Hardening function.
Materials
Material 1 (mat1)
1
In the Model Builder window, expand the Interpolated Hardening and User Defined Plastic Flow node, then click Component 1 (comp1)>Materials>Material 1 (mat1).
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Hardening function
sigmagh
hardening
Pa
Elastoplastic material model
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Stationary.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2
Step 1: Stationary
1
In the Settings window for Stationary, locate the Study Extensions section.
2
Select the Auxiliary sweep check box.
3
Click  Add.
4
In the table, enter the following settings:
Parameter name
Parameter value list
para (Horizontal load parameter)
0 range(0.40,0.05,2.2)
The solver settings are the same as in the previous study.
5
In the Model Builder window, click Study 2.
6
In the Settings window for Study, type Interpolated Hardening and User Defined Plastic Flow in the Label text field.
7
In the Home toolbar, click  Compute.
Results
Stress, Interpolated Hardening and User Defined Plastic Flow
The first default plot of the second study shows the von Mises stress for the final parameter value.
1
In the Settings window for 2D Plot Group, type Stress, Interpolated Hardening and User Defined Plastic Flow in the Label text field.
Plastic Region, Interpolated Hardening and User Defined Plastic Flow
1
In the Model Builder window, under Results click Equivalent Plastic Strain (solid).
2
In the Settings window for 2D Plot Group, type Plastic Region, Interpolated Hardening and User Defined Plastic Flow in the Label text field.
Contour 1
1
In the Model Builder window, expand the Plastic Region, Interpolated Hardening and User Defined Plastic Flow node, then click Contour 1.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type solid.epeGp>0.
The analysis is now finished. If you want to store this model and re-use it later, you will need to disable the second plasticity feature for the first study.
Linear Hardening
Step 1: Stationary
1
In the Model Builder window, under Linear Hardening click Step 1: Stationary.
2
In the Settings window for Stationary, locate the Physics and Variables Selection section.
3
Select the Modify model configuration for study step check box.
4
In the tree, select Component 1 (Comp1)>Solid Mechanics (Solid)>Linear Elastic Material 1>Interpolated Hardening and User Defined Plastic Flow.
5
Right-click and choose Disable.