
|
|
•
|
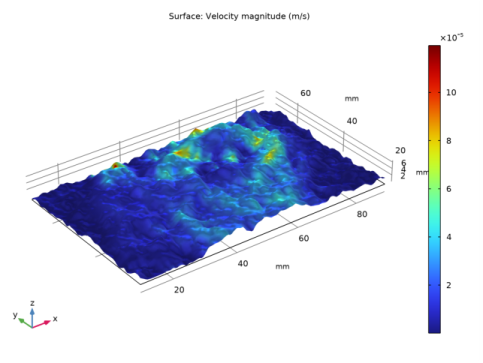
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
|
5
|
|
6
|
|
7
|
Click
|
|
8
|
|
9
|
Click OK.
|
|
10
|
|
11
|
|
12
|
Click
|
|
13
|
|
14
|
Click OK.
|
|
15
|
|
16
|
|
17
|
Click
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Click
|
|
5
|
Browse to the model’s Application Libraries folder and double-click the file rock_fracture_flow_aperture_data.txt.
|
|
6
|
Click
|
|
7
|
Find the Functions subsection. In the table, enter the following settings:
|
|
8
|
|
9
|
In the Function table, enter the following settings:
|
|
10
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Convection-Diffusion Equation (cdeq) click Convection-Diffusion Equation 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
3
|
In the Settings window for Dirichlet Boundary Condition, locate the Dirichlet Boundary Condition section.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
7
|
|
8
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
12
|
|
1
|
In the Model Builder window, under Component 2 (comp2) right-click Definitions and choose Variables.
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1.
|
|
5
|
|
6
|
In the Dependent variables table, enter the following settings:
|
|
7
|
Click the Units tab.
|
|
8
|
|
9
|
|
10
|
Click
|
|
11
|
|
12
|
Click OK.
|
|
13
|
|
14
|
|
15
|
In the Physical Quantity dialog box, select Transport>Time change in pressure head (m/s) in the tree.
|
|
16
|
Click OK.
|
|
17
|
|
18
|
|
1
|
In the Model Builder window, under Component 2 (comp2)>Coefficient Form Boundary PDE (cb) click Coefficient Form PDE 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
|
3
|
In the Settings window for Dirichlet Boundary Condition, locate the Dirichlet Boundary Condition section.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Convection-Diffusion Equation (cdeq).
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|