
|
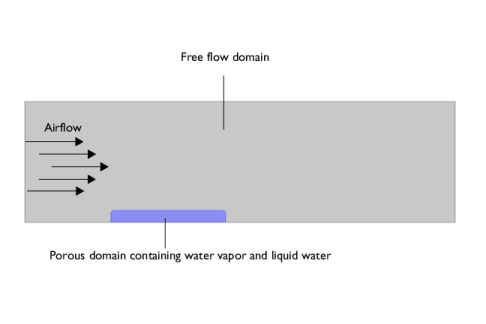
|
•
|
Convection of vapor due to total pressure gradient, with the flow field ug computed by the Brinkman equation.
|
|
•
|
Convection of liquid water due to total pressure gradient, with the flow field ul computed by the Darcy’s Law in Equation 2. The permeability for the liquid phase κl depends on the overall permeability of the porous matrix κ and a relative permeability (see Permeability) κrl.
|
|
•
|
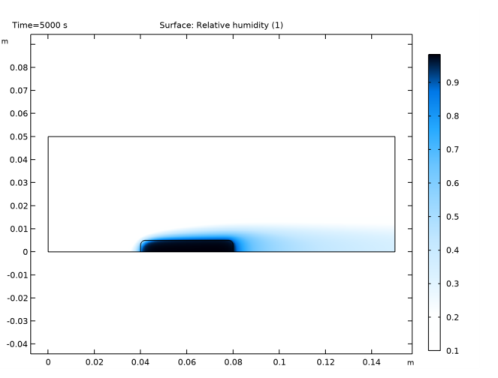
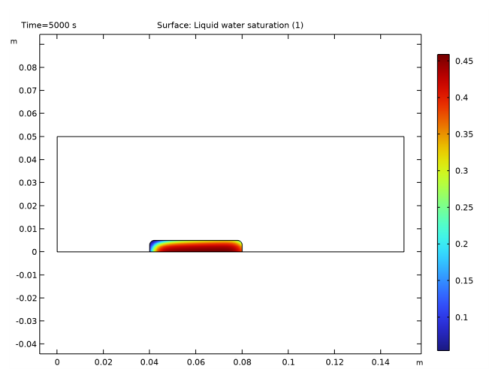

|
1
|
|
2
|
In the Select Physics tree, select Heat Transfer>Heat and Moisture Transport>Heat and Moisture Flow>Laminar Flow.
|
|
3
|
Click Add.
|
|
4
|
Click
|
|
5
|
|
6
|
Click
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file potato_drying_parameters.txt.
|
|
1
|
|
2
|
|
3
|
In the Settings window for Piecewise, type Relative Permeability, Moist Air in the Label text field.
|
|
4
|
|
5
|
|
6
|
Find the Intervals subsection. In the table, enter the following settings:
|
|
7
|
|
1
|
|
2
|
In the Settings window for Piecewise, type Relative Permeability, Liquid Phase in the Label text field.
|
|
3
|
|
4
|
|
5
|
Find the Intervals subsection. In the table, enter the following settings:
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Browse to the model’s Application Libraries folder and double-click the file potato_drying_wc.txt.
|
|
6
|
|
7
|
In the Function table, enter the following settings:
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
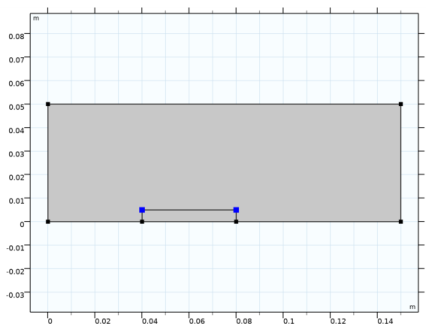
On the object r2, select Points 3 and 4 only.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Heat Transfer in Moist Air (ht) click Initial Values 1.
|
|
2
|
|
3
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Moisture Transport in Air (mt) click Initial Values 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
In the Settings window for Hygroscopic Porous Medium, locate the Moisture Transport Properties section.
|
|
4
|
|
1
|
In the Model Builder window, expand the Hygroscopic Porous Medium 1 node, then click Liquid Water 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose More Materials>Porous Material.
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
Click OK.
|
|
1
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
In the table, clear the Solve for check boxes for Moisture Transport in Air (mt) and Heat Transfer in Moist Air (ht).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for 1D Plot Group, type Moisture Content in Porous Medium over Time in the Label text field.
|
|
1
|
|
2
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Moisture Transport in Air>Mass balance>mt.massBalance - Mass balance - kg/s.
|
|
4
|
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Moisture Transport in Air>Mass balance>mt.dwcInt - Total accumulated moisture rate - kg/s.
|
|
5
|
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Moisture Transport in Air>Mass balance>mt.ntfluxInt - Total net moisture rate - kg/s.
|
|
6
|
Click Add Expression in the upper-right corner of the Expressions section. From the menu, choose Component 1 (comp1)>Moisture Transport in Air>Mass balance>mt.GInt - Total mass source - kg/s.
|
|
7
|
Click
|
|
1
|
Go to the Table window.
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|