PDF
Copper Deposition in a Trench Using
the Level Set Method
Introduction
This model example is based on the Copper Deposition in a Trench model, available in the Electrodeposition Module Application Library, which demonstrates that there is a nonuniform deposition along the trench surface, leading to formation of a cavity or void (Ref. 1). Because the Copper Deposition in a Trench model uses the Deformed Geometry node, which cannot handle topological changes, the computations cannot be continued once the cavity is formed at around 14 s.
The model example presented here uses the Level Set interface instead of the Deformed Geometry node. The Level Set interface can handle topological changes. In the present model, computations are performed for up to 20 s, well beyond the time for cavity formation.
Model Definition
The deposition process is inherently time-dependent because the cathode boundary moves as the deposition process takes place. The model is defined by the material balances for the involved ions (copper, Cu2+, and sulfate, SO42-) and by the electroneutrality condition.
The model geometry is shown in Figure 1. The upper horizontal boundary represents the anode, while the cathode is placed at the bottom. The vertical walls are assumed to be insulating.
Figure 1: Model domain with boundaries corresponding to the anode, cathode, and vertical symmetry walls.
When using the Level Set method, both the electrode and the electrolyte are described on the same domain. The Level Set interface is used to keep track of the deformation at the cathode surface during deposition. For simplicity, the anode position is kept fixed in this model. The Level Set interface automatically sets up the equations for the movement of the interface between the liquid electrolyte and the solid electrode. The interface is represented by the 0.5 contour of the level set variable . The level set variable varies from 1, in the electrolyte domain, to 0, in the deposited region. The level set variable can thus be thought of as the electrolyte volume fraction. The transport of the level set variable is given by:
The ε parameter determines the thickness of the interface and is defined as ε = hmax/4, where hmax is the maximum mesh element size in the domain. The γ parameter determines the amount of reinitialization. A suitable value for γ is the maximum velocity magnitude occurring in the model.
The level set delta function is approximated by:
The velocity field used in the transport equation for level set variable is evaluated from the copper deposition reaction current density:
where iloc is the local current density, MCu is the molar mass and ρCu is the density of copper.
The interface normal n is calculated as:
The level set variable of value 0 enters the domain from the bottommost boundaries of the domain, which are prescribed using the Inlet boundary condition. The rest of the boundaries are prescribed using the Outlet boundary condition.
The usage of the Level Set method means that the balance equations have to be modified in comparison with those used in the Copper Deposition in a Trench model. First, the flux for each of the ions in the electrolyte is given by the Nernst-Planck equation with effective diffusion coefficients and mobilities,
where Ni denotes the transport vector (mol/(m2·s)), ci the concentration in the electrolyte (mol/m3), zi the charge for the ionic species, ui,eff the mobility of the charged species (m2/(s·J·mole)), F Faraday’s constant (As/mole), and the potential in the electrolyte (V). The effective diffusion coefficients are defined using the electrolyte volume fraction:
where is the electrolyte volume fraction. is defined in terms of the level set variable, and varies from 1 in the electrolyte domain and 0 in the deposited region. The effective diffusion coefficients ensure that the fluxes of the ions are equal to 0 where the level set variable is 0.
Furthermore, the material balances are expressed through
one for each species, that is i = 1, 2.
The rate of electrochemical reaction is
The electrolyte volume fraction compensation ensures that the electrode will not act as a reservoir for the copper and sulfate ions.
The electroneutrality condition is given by the following expression:
The deposition process is assumed to take place through the following simplified mechanism:
where the first step is rate determining step, RDS, and the second step is assumed to be at equilibrium (Ref. 1). This gives the following the Butler-Volmer equation for the local current density as a function of potential and copper concentration:
where η denotes the overpotential defined as
where denotes the electronic potential of the respective electrode.
The copper deposition reaction current density at the cathode surface is added as a source term in the domain, using the level set delta function to prescribe the deposition reaction along the deforming boundary:
The boundary condition at the anode surface is:
where n denotes the normal vector to the boundary. For simplicity, the anode surface is not deformed in this model.
All other boundaries are insulating:
For the sulfate ions, insulating conditions apply everywhere:
The initial conditions set the composition of the electrolyte according to
The electrochemical model described above is set up using the Tertiary Current Distribution, Nernst-Planck Equations interface.
Results and Discussion
Figure 2 shows surface plots of the electrolyte potential and the level set variable after 20 s of deposition operation. The surface plot of the level set variable, plotted using a gray scale, represents the copper deposition region where its value is less than 0.5. It can be seen that there is a nonuniform deposition along the trench (cathode) surface. The deposition rate is higher near mouth of the trench than at the bottom of the trench, leading to formation of a cavity or void. The isolated cavity can be detrimental to the quality of the deposition because a trapped electrolyte can later cause corrosion of components in the circuit board.
The electrolyte potential in the cavity relaxes so that the electrode potential () corresponds to the resulting equilibrium potential (Eeq) for the concentration in the cavity, leading the local current density value to 0 inside the cavity.
Figure 2: Surface plot of electrolyte potential along with the level set variable contour of value 0.5 after 20 seconds of deposition operation.
Figure 3 shows the surface plots of the corresponding concentration of copper ions and the level set variable after 20 s of deposition operation. The simulation shows substantial variations in copper ion concentration in the cell. Such variations eventually cause free convection in the cell. The nonuniform deposition rate at the cathode surface is attributed to nonuniform electrolyte current distribution which is accentuated by the depletion of copper ions at the bottom of the trench.
Figure 3: Surface plot of concentration of copper ions along with the level set variable contour of value 0.5 after 20 seconds of deposition operation.
In Figure 4 and Figure 5 we now compare the results obtained from the Level Set interface in this model with those obtained from the Deformed Geometry node in the Copper Deposition in a Trench model, after 14 s of deposition operation (which corresponds to the time close to the cavity formation)
Figure 4: Surface plot of concentration of copper ions along with the level set variable contour of value 0.5 after 14 seconds of deposition operation using the Level Set interface.
Figure 5: Surface plot of the concentration distribution of copper ions, the isopotential lines, the current density lines, and the displacement of the cathode and anode surfaces after14 seconds of deposition operation using the Deformed Geometry node.
It can be seen from Figure 4 and Figure 5 that the deposition profile and the concentration distribution of copper ions obtained from the Level Set interface match well with the same obtained from the Deformed Geometry node. Some minor differences can be seen in the plots with regards to concentrations and position of the moving cathode. These can mainly be attributed to the anode position, which is allowed to move in Figure 5, but is fixed in Figure 4.
In conclusion, electrodeposition models using the level set method can be useful in identifying cavity or void regions formed during a deposition process in complex geometries.
Reference
1. E. Mattsson and J.O’M. Bockris, “Galvanostatic Studies of the Kinetics of Deposition and Dissolution in the Copper + Copper Sulphate System”, Trans. Far. Soc., vol. 55, p. 1586, 1959.
Application Library path: Electrodeposition_Module/Tutorials/cu_trench_deposition_ls
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D.
2
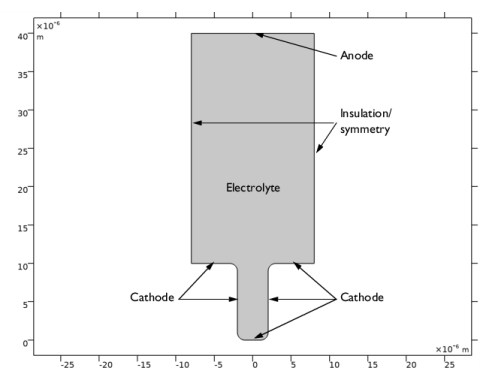
In the Select Physics tree, select Electrochemistry>Tertiary Current Distribution, Nernst-Planck>Tertiary, Electroneutrality (tcd).
3
Click Add.
4
In the Concentrations table, enter the following settings:
cCu
cSO4
5
In the Select Physics tree, select Mathematics>Moving Interface>Level Set (ls).
6
Click Add.
7
Click  Study.
8
In the Select Study tree, select Preset Studies for Some Physics Interfaces>Time Dependent with Initialization.
9
Click  Done.
Geometry 1
Draw the geometry by making a union of two rectangles. Round off the corners of the trench using fillets.
Rectangle 1 (r1)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 1.6e-5.
4
In the Height text field, type 3e-5.
5
Locate the Position section. In the x text field, type -0.8e-5.
6
In the y text field, type 1e-5.
Rectangle 2 (r2)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 0.4e-5.
4
In the Height text field, type 1e-5.
5
Locate the Position section. In the x text field, type -0.2e-5.
6
Click  Build Selected.
7
Click the  Zoom Extents button in the Graphics toolbar.
Union 1 (uni1)
1
In the Geometry toolbar, click  Booleans and Partitions and choose Union.
2
In the Settings window for Union, locate the Union section.
3
Clear the Keep interior boundaries check box.
4
Click in the Graphics window and then press Ctrl+A to select both objects.
Fillet 1 (fil1)
1
In the Geometry toolbar, click  Fillet.
2
On the object uni1, select Points 3–6 only.
3
In the Settings window for Fillet, locate the Radius section.
4
In the Radius text field, type 1e-6.
Form Union (fin)
1
In the Model Builder window, click Form Union (fin).
2
In the Settings window for Form Union/Assembly, click  Build Selected.
Global Definitions
Load the model parameters from a text file.
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file cu_trench_deposition_ls_parameters.txt.
Definitions
Load the model variables from a text file.
Variables 1
1
In the Home toolbar, click  Variables and choose Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file cu_trench_deposition_ls_variables.txt.
Tertiary Current Distribution, Nernst-Planck (tcd)
Now set up the electrochemical model, consisting of a Highly Conductive Porous Electrode domain and an electrode boundary.
Highly Conductive Porous Electrode 1
1
In the Model Builder window, under Component 1 (comp1) right-click Tertiary Current Distribution, Nernst-Planck (tcd) and choose Highly Conductive Porous Electrode.
2
In the Settings window for Highly Conductive Porous Electrode, locate the Domain Selection section.
3
From the Selection list, choose All domains.
4
Locate the Diffusion section. In the DcCu text field, type D_Cu.
5
In the DcSO4 text field, type D_SO4.
6
Locate the Migration in Electric Field section. In the zcCu text field, type z_Cu.
7
In the zcSO4 text field, type z_SO4.
Set the electrolyte volume fraction to epsl. This implies that all the volume of the modeled domain belongs to the electrolyte phase.
8
Locate the Porous Matrix Properties section. In the εl text field, type epsl.
Set the effective transport parameter correction for diffusion to user defined and set the correction factor to epsl so that the correction is applied only in the electrolyte phase excluding the deposited region.
9
Locate the Effective Transport Parameter Correction section. From the Diffusion list, choose User defined. In the fDl text field, type epsl.
10
Locate the Electrode Phase Potential Condition section. In the φs,ext text field, type phis_cathode.
Porous Electrode Reaction 1
Set up the copper deposition electrode reaction kinetics parameters.
1
In the Model Builder window, click Porous Electrode Reaction 1.
2
In the Settings window for Porous Electrode Reaction, locate the Stoichiometric Coefficients section.
3
In the n text field, type 2.
4
Locate the Equilibrium Potential section. From the Eeq list, choose User defined. In the associated text field, type Eeq_rel.
5
Locate the Electrode Kinetics section. From the Kinetics expression type list, choose Concentration dependent kinetics.
6
In the i0 text field, type i0.
7
In the αa text field, type alpha_a.
8
In the αc text field, type alpha_c.
9
In the CO text field, type cCu/Cinit.
10
Locate the Active Specific Surface Area section. In the av text field, type ls.delta.
Electrode Surface 1
Define the electrode kinetics at the anode surface.
1
In the Physics toolbar, click  Boundaries and choose Electrode Surface.
2
Select Boundary 3 only.
3
In the Settings window for Electrode Surface, locate the Electrode Phase Potential Condition section.
4
In the φs,ext text field, type phis_anode.
5
Click to expand the Dissolving-Depositing Species section. Click  Add.
6
In the table, enter the following settings:
Species
Density (kg/m^3)
Molar mass (kg/mol)
cdep_anode
8960
0.06355
Electrode Reaction 1
1
In the Model Builder window, click Electrode Reaction 1.
2
In the Settings window for Electrode Reaction, locate the Stoichiometric Coefficients section.
3
In the n text field, type 2.
4
Locate the Electrode Kinetics section. In the i0,ref(T) text field, type i0.
5
In the αa text field, type alpha_a.
Initial Values 1
Set the initial concentration of copper and sulfate ions.
1
In the Model Builder window, under Component 1 (comp1)>Tertiary Current Distribution, Nernst-Planck (tcd) click Initial Values 1.
2
In the Settings window for Initial Values, locate the Initial Values section.
3
In the cSO4 text field, type Cinit.
Level Set (ls)
Now, set up the Level Set model.
1
In the Model Builder window, under Component 1 (comp1) click Level Set (ls).
2
In the Settings window for Level Set, click to expand the Discretization section.
3
From the Level set variable list, choose Quadratic.
Level Set Model 1
Next, specify the reinitialization parameter, parameter controlling interface thickness and velocity field.
1
In the Model Builder window, under Component 1 (comp1)>Level Set (ls) click Level Set Model 1.
2
In the Settings window for Level Set Model, locate the Level Set Model section.
3
In the γ text field, type max(Vn,eps).
4
In the εls text field, type ls.hmax/4.
5
Locate the Convection section. Specify the u vector as
Vn*ls.intnormx
x
Vn*ls.intnormy
y
Initial Values 1
Set the initial value of the level set variable to 1.
1
In the Model Builder window, click Initial Values 1.
2
In the Settings window for Initial Values, locate the Initial Values section.
3
Click the Fluid 2 (ϕ = 1) button.
Inlet 1
Define inlet and outlet boundaries for the level set variable.
1
In the Physics toolbar, click  Boundaries and choose Inlet.
2
Select Boundaries 2, 4–7, and 9–12 only.
Outlet 1
1
In the Physics toolbar, click  Boundaries and choose Outlet.
2
Select Boundaries 1, 3, and 8 only.
Global Definitions
Default Model Inputs
Set up the temperature value used in the entire model.
1
In the Model Builder window, under Global Definitions click Default Model Inputs.
2
In the Settings window for Default Model Inputs, locate the Browse Model Inputs section.
3
In the tree, select General>Temperature (K) - minput.T.
4
Find the Expression for remaining selection subsection. In the Temperature text field, type T0.
Mesh 1
Now make the settings for the mesh.
Size
1
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Edit Physics-Induced Sequence.
2
In the Settings window for Size, locate the Element Size section.
3
From the Predefined list, choose Normal.
Refine 1
1
In the Mesh toolbar, click  Modify and choose Refine.
2
In the Settings window for Refine, click to expand the Refine Elements in Box section.
3
Select the Specify bounding box check box.
4
In row x, set Lower bound to -1E-5.
5
In row x, set Upper bound to 1E-5.
6
In row y, set Lower bound to -8E-7.
7
In row y, set Upper bound to 2E-5.
8
Click  Build All.
Your finished mesh should now look like this:
Study 1
Modify the solver settings to simulate the deposition process during 20 s, storing the solution every 0.5 s. Use the initial valued based scaling and clear generate default plots option and then start the computation.
Step 2: Time Dependent
1
In the Model Builder window, under Study 1 click Step 2: Time Dependent.
2
In the Settings window for Time Dependent, locate the Study Settings section.
3
In the Output times text field, type range(0,0.5,20).
Solution 1 (sol1)
1
In the Study toolbar, click  Show Default Solver.
2
In the Model Builder window, expand the Solution 1 (sol1) node, then click Dependent Variables 2.
3
In the Settings window for Dependent Variables, locate the Scaling section.
4
From the Method list, choose Initial value based.
5
In the Model Builder window, click Study 1.
6
In the Settings window for Study, locate the Study Settings section.
7
Clear the Generate default plots check box.
8
In the Study toolbar, click  Compute.
Results
The following steps reproduce the plots from the Results and Discussion section.
Electrolyte Potential (tcd)
1
In the Home toolbar, click  Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type E in the Label text field.
3
In the Label text field, type Electrolyte Potential (tcd).
Surface 1
In the Electrolyte Potential (tcd) toolbar, click  Surface.
Filter 1
1
In the Electrolyte Potential (tcd) toolbar, click  Filter.
2
In the Settings window for Filter, locate the Element Selection section.
3
In the Logical expression for inclusion text field, type phils>0.5.
Surface 2
1
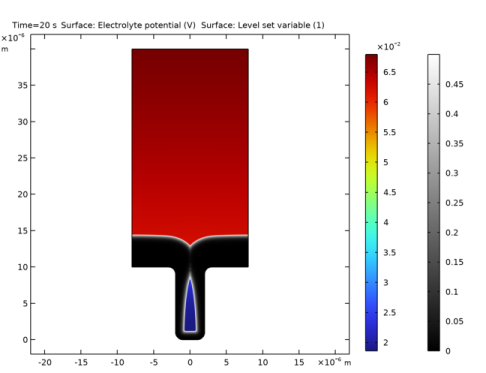
In the Model Builder window, under Results>Electrolyte Potential (tcd) right-click Surface 1 and choose Duplicate.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type phils.
4
Locate the Coloring and Style section. From the Color table list, choose GrayScale.
Filter 1
1
In the Model Builder window, expand the Surface 2 node, then click Filter 1.
2
In the Settings window for Filter, locate the Element Selection section.
3
In the Logical expression for inclusion text field, type phils<0.5.
4
In the Electrolyte Potential (tcd) toolbar, click  Plot.
Electrolyte Potential (tcd)
Now, plot the concentration of copper ions by making use of the Duplicate functionality.
Concentration (tcd)
1
In the Model Builder window, right-click Electrolyte Potential (tcd) and choose Duplicate.
2
In the Model Builder window, click Electrolyte Potential (tcd) 1.
3
In the Settings window for 2D Plot Group, type Concentration (tcd) in the Label text field.
Surface 1
1
In the Model Builder window, click Surface 1.
2
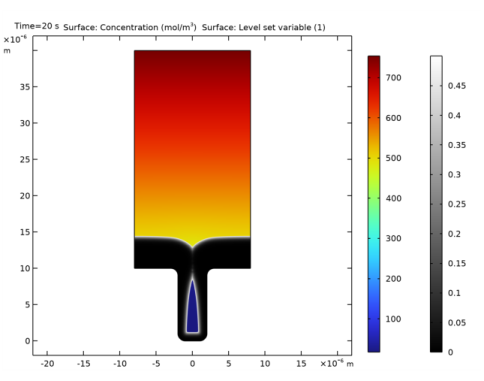
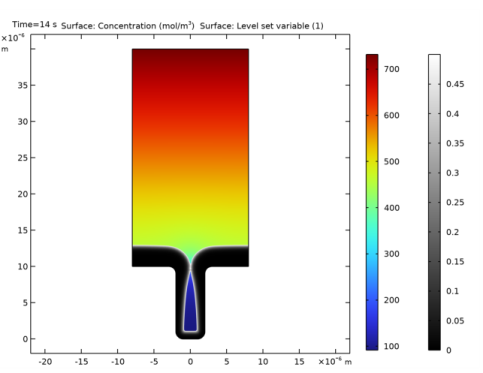
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1)>Tertiary Current Distribution, Nernst-Planck>Species cCu>cCu - Concentration - mol/m³.
3
In the Concentration (tcd) toolbar, click  Plot.
Concentration (tcd)
Now, plot the concentration of copper ions at 14 s to compare the results with the deformed geometry formulation.
1
In the Model Builder window, click Concentration (tcd).
2
In the Settings window for 2D Plot Group, locate the Data section.
3
From the Time (s) list, choose 14.
4
In the Concentration (tcd) toolbar, click  Plot.