Packed Bed Reactor

The packed bed reactor is used in heterogeneous catalytic processes and is one of the most common reactors in chemical industry. Its basic design is a column filled with porous catalyst particles, and these particles can be contained within a supporting structure, such as tubes or channels, or they can be packed in one single compartment in the reactor. In this example, volatile organic compounds (VOC) and CO are oxidized in a catalytic converter. Propylene is used as a representative for hydrocarbons present in the feed stream, which could, for example, be exhaust gas from a combustion process.

The structure of the packed catalyst particles makes the modeling of mass and energy transport in the reactor a challenge. The difficulty lies in the description of the porous structure, which gives transport of different orders of magnitudes within and between the particles. In most cases the structure in between particles is described as macroporous and the particle radius can be of the order of magnitude of 1 mm. When a pressure difference is applied across the bed, convection arises in the macropores. The pores inside the catalyst particles form the microstructure of the bed. The pore radii in the particles is often between 1 and 10 micrometers.

Figure 1: An example of the macro dimension (bed height) and the microdimension (pellet radial position) in a packed bed reactor.

This model presents a multigeometry approach to study microscale and macroscale mass balances in packed beds and other heterogeneous reactors with bimodal pore distribution. The example provides the mass and reaction distributions along the reactor and within each catalyst pellet along the reactor length. The Transport of Diluted Species and Chemistry interfaces are used and enable evaluation of the catalyst load utilization, optimal pellet size, or inlet temperature.

Model Definition

The following chemical reactions describe oxidation of carbon monoxide and an organic volatile by-product such as propylene in an automobile catalytic converter:

(1)

(2)

For these heterogeneous catalytic reactions the rates (SI unit: mol/(m3·s)) are given by (Ref. 2):

The rate and adsorption constants are defined by Arrhenius expressions which are available in the Chemistry interface. The values of the frequency factors and activation energies (SI unit: J/mol) are taken from the literature (Ref. 3) and listed in Table 1,

Table 1: Arrhenius parameters.
Rate/Adsorption Constant	Frequency factor	Activation energy (Joule/mol)
k1	7.07·1013	1.09·105
k2	1.47·1015	1.26·105
KCO	8.1	-3400
KC3H6	257.9	1588

The chemical reactions in Equation 1 and Equation 2 describe a process limited by the second-order rate expression at high temperatures when the surface coverage is low. At low temperatures the adsorption reactions are slower and limit the reaction rate due to a shortage of free catalytic sites.

Macroscale Equations

The pressure drop along the reactor is described by the Ergun equation and is solved with a Coefficient Form PDE:

(3)

In Equation 3, P is the pressure (SI unit: Pa), εb the porosity, Dp the particle diameter (SI unit: m), μ denotes the gas viscosity (SI unit: Pa·s), ρ the gas density (SI unit: kg/m3), and x the reactor length coordinate (SI unit: m). u is the reactor flow velocity (SI unit: m/s) that depends on the pressure and velocity of the feed (SI unit: m/s), as described by Equation 4:

(4)

This relation applies since the flux across the reactor is set as constant, the system is assumed to be isothermal, and the fluid (air) is considered to be an ideal gas.

The mass transport on the macroscale level, along the reactor, takes place through convection and diffusion. This is easily accounted for using the Transport of Diluted Species interface in which the following equation (stationary) is solved:

(5)

The reaction rate R source term (SI unit: mol/(m3·s)) in Equation 5 depends on the transport inside the catalyst particles. The molar flux at the outer surface of the particles multiplied by the available outer surface area of the particles per unit volume gives the proper source term:

(6)

In Equation 6, εb is the bed porosity, N denotes the flux vector inside the porous particle (SI unit: mol/(m2·s)) and n is the outward unit vector normal to the particle surface. The equation is only valid at the particle surface, where the independent radius variable r (introduced below) equals the particle radius, rp. Furthermore, Ap denotes the pellet surface to volume ratio (SI unit: m2/m3). This property is related to the pellet radius as:

The boundary conditions for the macroscale mass balances are as follows:

At the inlet, the reactant concentrations are known:

cCO = cCOin

cC3H6 = cC3H6in

cO2 = cO2in

cCO2 = 0

cH2O = 0

At the outlet, the Outflow condition states that convective mass transport dominates the species transport across the boundary.

Microscale Equations

To properly calculate R, mass balances are required for the catalyst pellet interior, that is, the microscale. In the catalyst pores, mass transport can be assumed to take place by diffusion only. If the pellets are selected with spherical and dimensionless coordinates the following equation applies:

(7)

Here, Dcp is the diffusion coefficient in the particle, cp is the species concentration in the particle, and Rp is the reaction rate for the heterogeneous reaction in the particle. r (SI unit: m) is the independent variable for the position along the radius of the particle. Equation 7 is modeled with a Transport of Diluted Species interface with corrections for spherical coordinates and dimensionless particle radius. The boundary conditions are symmetry at the center of the particle and concentration at the surface. The latter is described by cp = εc where c and cp represent the species concentrations in the bulk and in the particle, respectively, and ε is the catalyst porosity. The concentration at the surface of the particle is equal to the concentration outside the particle compensated to account for the part of the particle volume that is occupied by solid catalyst support.

The concentration distribution in the particle gives the molar flux at every point along the reactor. This implies that the source term (Equation 6) in the macroscale mass balance becomes:

This type of problem exists for many chemical reaction engineering applications and is often solved by using an analytical approximation of the solution to the microscale mass balance. However, such an approach cannot be used for complicated reaction mechanisms involving several reaction species. The approach shown here is general and can be used for very complex reaction mechanisms involving a large number of species.

Macroscale and Microscale implementation

A complication in solving the derived system of equations is that the macroscale and microscale balances are defined in different coordinate systems. In this example, the macroscale part (along the reactor length) is set up in 1D and the microscale (along the pellet radius) in 2D. In the latter part, the x direction represents the surface concentration of the pellet at each part along the reactor and the y direction the concentration distribution along the dimensionless pellet radius.

To achieve the coupling of the fluxes and concentrations between the two scales of the system, general extrusion features are used.

Results and Discussion

Figure 2 shows the concentration of reacting species as a function of position in the reactor. The levels of carbon monoxide and propylene are significantly reduced.

Figure 2: The concentration of reactants and products along the reactor length. The pellet radius rp is 2.5 mm.

The concentration can also be evaluated within each pellet, revealing whether or not the catalyst comes to efficient use. Figure 3 is an example of this.

Figure 3: The concentration of in-pellet CO as a function of reactor position. The scaled pellet radius is given on the y-axis and the reactor position along the x-axis.

From Figure 3 it is clear that the CO concentration is low at the center of the pellet at all reactor positions. This means that reactor performance is limited by diffusion within the pellets and that active catalyst material in the center of the pellet is not used. Reducing the pellet diameter could potentially fix this situation and simulation results (see Figure 4) confirm this.

With a pellet radius of 2.5 mm, the reactor is limited by the in-pellet diffusion, as is indicated by the slope of the solid lines. The effect of this is that the active sites in the interior of the pellets are not used to their full potential. If the pellet size is reduced (represented by the lines with a triangular marker) the lines level out faster, suggesting larger reaction limited regions.

Figure 4: The concentration of in-pellet C3H6 at different reactor positions (5, 15, and 25 cm). Solid lines represent a pellet radius of 2.5 mm and lines with triangular markers represent a pellet radius of 1.8 mm.

References

1. J.M. Coulson and J.F. Richardson, Chemical Engineering, vol. 2, 4th ed., Pergamon Press, 1990.

2. S.H. Oh, J.C. Cavendish, and L.L. Hegedus. “Mathematical modeling of catalytic converter lightoff: Single-pellet studies”, AIChE Journal, vol. 26, no. 6, pp. 935–943, 1980.

3. J.B. Rawlings and J.G. Ekerdt, Chemical Reactor Analysis and Design Fundamentals, Nob Hill Publishing, Madison, 2002.

Chemical_Reaction_Engineering_Module/Reactors_with_Porous_Catalysts/packed_bed_reactor

Modeling Instructions

From the menu, choose .

New

In the window, click

Model Wizard

In the window, Start by adding the necessary 1D physics interfaces: and .

click

In the tree, select .

Click .

In the text field, type 5.

In the table, enter the following settings:


C3H6
CO
CO2
H2O
O2

In the tree, select .

Click .

In the text field, type P.

In the table, enter the following settings:


P

Click

In the tree, select .

Click

Geometry 1

Interval 1 (i1)

In the window, under right-click and choose .

In the window for , locate the section.

In the table, enter the following settings:


Coordinates (m)
0
0.3

Click

Root

Add the model parameters from a text file.

Global Definitions

Parameters 1

In the window, under click .

In the window for , locate the section.

Click

Browse to the model’s Application Libraries folder and double-click the file packed_bed_reactor_parameters.txt.

Variables 1

In the toolbar, click

and choose .

Import also the global variables from a text file.

In the window for , locate the section.

Click

Browse to the model’s Application Libraries folder and double-click the file packed_bed_reactor_variables_global.txt.

Follow these steps to set up mass transport equations for the packed bed. Start with the .

Transport of Diluted Species (tds)

Transport Properties 1

In the window, under click .

In the window for , locate the section.

Specify the u vector as


u	x

Locate the section. In the DC3H6 text field, type D_C3H6.

In the DCO text field, type D_CO.

In the DCO2 text field, type D_CO2.

In the DH2O text field, type D_H2O.

In the DO2 text field, type D_O2.

Initial Values 1

In the window, click .

In the window for , locate the section.

In the C3H6 text field, type 1e-6.

In the CO text field, type 1e-6.

In the CO2 text field, type 1e-6.

In the H2O text field, type 1e-6.

In the O2 text field, type 1e-6.

Reactions 1

In the toolbar, click

and choose .

Select Domain 1 only.

In the window for , locate the section.

In the RC3H6 text field, type -Ap*C3H6flux*(1-por_b).

In the RCO text field, type -Ap*COflux*(1-por_b).

In the RCO2 text field, type -Ap*CO2flux*(1-por_b).

In the RH2O text field, type -Ap*H2Oflux*(1-por_b).

In the RO2 text field, type -Ap*O2flux*(1-por_b).

You will define the flux variables later on, after having set up the pellet model. Note that the volume fraction of the catalytic particles in the reactor is (1-por_b).

Inflow 1

In the toolbar, click

and choose .

Select Boundary 1 only.

In the window for , locate the section.

In the c0,C3H6 text field, type x_C3H6_feed*Ctot_feed.

In the c0,CO text field, type x_CO_feed*Ctot_feed.

In the c0,O2 text field, type x_O2_feed*Ctot_feed.

Locate the section. From the list, choose .

Outflow 1

In the toolbar, click

and choose .

Select Boundary 2 only.

Coefficient Form PDE: Ergun Equation

Follow the steps below to specify the Ergun equation in the .

In the window, under click .

In the window for , type Coefficient Form PDE: Ergun Equation in the text field.

Locate the section. Click

In the dialog box, type pressure in the text field.

Click

In the tree, select .

Click .

In the window for , locate the section.

In the table, enter the following settings:


Source term quantity	Unit
Custom unit	N/m^3

Coefficient Form PDE 1

In the window, under click .

In the window for , locate the section.

In the c text field, type 0.

Locate the section. In the f text field, type Px+(150*mu*u/(2*Rr)^2*(1-por_b)^2/por_b^3+1.75*rho_feed*u^2/(2*Rr)*(1-por_b)/por_b^3).

Locate the section. In the da text field, type 0.

Initial Values 1

In the window, click .

In the window for , locate the section.

In the P text field, type P_feed.

Dirichlet Boundary Condition 1

In the toolbar, click

and choose .

Select Boundary 1 only.

In the window for , locate the section.

In the r text field, type P_feed.

The source terms in the reactor mass balances depend on the surface fluxes from the catalyst pellets. Therefore, set up a separate model component calculating the mass transport and reaction in the pellets.The model geometry is in 2D. The x-coordinate represents reactor length and the y-coordinate the pellet radius.

Add Component

In the window, right-click the root node and choose .

Add Physics

In the toolbar, click

to open the window.

Go to the window.

Select a interface handling the reactions and a interface for the mass transport within the pellets.

In the tree, select .

Click in the window toolbar.

In the tree, select .

Click to expand the section. In the text field, type 5.

In the table, enter the following settings:


C3H6p
COp
CO2p
H2Op
O2p

Click in the window toolbar.

In the toolbar, click

to close the window.

Geometry 2

Square 1 (sq1)

In the toolbar, click

In the window for , click

Chemistry (chem)

Start setting up the interface for the two reactions present in the system.

In the window, under click .

Reaction 1

In the toolbar, click

and choose .

In the window for , locate the section.

In the text field, type CO+1/2O2=>CO2.

Click .

Locate the section. In the rj text field, type chem.kf_1*chem.c_CO*chem.c_O2/(1+KCO*chem.c_CO+KC3H6*chem.c_C3H6)^2.

Find the subsection. In the text field, type 2.

Locate the section. Select the check box.

In the Af text field, type A1.

In the Ef text field, type E1.

Reaction 2

In the toolbar, click

and choose .

In the window for , locate the section.

In the text field, type C3H6+9/2O2=>3H2O+3CO2.

Click .

Locate the section. Find the subsection. In the text field, type 2.

In the rj text field, type chem.kf_2*chem.c_C3H6*chem.c_O2/(1+KCO*chem.c_CO+KC3H6*chem.c_C3H6)^2.

Locate the section. Select the check box.

In the Af text field, type A2.

In the Ef text field, type E2.

Species 1

In the toolbar, click

and choose .

In the window for , locate the section.

In the text field, type N2.

Locate the section. From the list, choose .

In the window, collapse the node.

Note that the molar masses are computed from the chemical formula.

In the window, click .

In the window for , locate the section.

From the T list, choose . In the associated text field, type Tr.

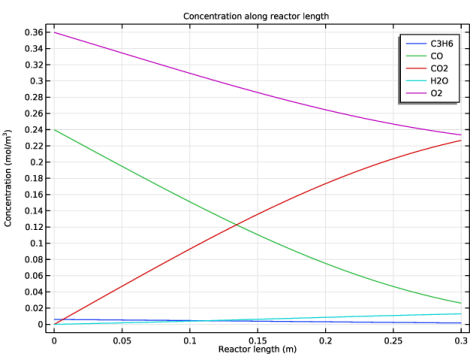
From the p list, choose . In the associated text field, type P_feed.

Locate the section. From the list, choose .

Find the subsection. In the table, enter the following settings:


Species	Type	Molar concentration	Value (mol/m^3)
C3H6	Variable	C3H6p	Solved for
CO	Variable	COp	Solved for
CO2	Variable	CO2p	Solved for
H2O	Variable	H2Op	Solved for
N2	Solvent	User defined	Cinert_feed
O2	Variable	O2p	Solved for