PDF
Flow Duct
Introduction
The modeling of aircraft-engine noise attenuation is a central problem in the field of computational aeroacoustics (CAA). In this example you simulate the harmonically time-varying acoustic field from a turbofan engine under various background flow conditions (a convected acoustic simulation) and calculate the attenuation of the acoustic noise made possible by introducing a layer of lining inside the engine duct. The noise is introduced as a source computed from a boundary mode analysis.
Model Definition
Assume that the flow in the axisymmetric duct is compressible, inviscid, perfectly isentropic, and irrotational. In this case the acoustic field is well described by the linearized potential flow equations. The Linearized Potential Flow, Frequency Domain interface is used to set up the model.
The flow is in this model described by Euler’s equations for an ideal gas (assuming adiabatic processes):
Here is the density, equals the velocity, denotes the pressure, equals the speed of sound, and γ is the constant ratio of the specific heats at constant pressure and volume. The variables are made dimensionless by division by suitable combinations of a reference duct radius R∞, a reference speed of sound c∞, and a reference density ρ∞.
Linearized Potential Flow Equations
Because the flow is assumed irrotational, you can describe the velocity field, , in terms of a potential , defined by the equation . The basic time- and space-dependent variables describing the flow are then the velocity potential and the density, . These variables (and the velocity field itself) are split into a stationary mean-flow part and a harmonically time-varying acoustic part:
where φ, v, and ρ are the acoustic variations to the potential, velocity, and density, respectively. Also assume that the amplitudes of the acoustic variables are small compared to the corresponding mean-flow quantities. This allows for a linearization of the equations of motion and the equation of state. The linearized potential flow equations for the acoustic variables are
For more theory information, see the aeroacoustics theory chapter in the Acoustics Module User’s Guide.
Geometry and Boundary Conditions
The duct geometry used in this model, shown in Figure 1, is taken from Ref. 1. It is an approximate model of the inlet section of a turbofan engine in the very common CFM56 series.
Figure 1: The duct geometry.
The spinner and duct-wall profiles are given, respectively, by the equations
where 0 ≤ z′ = z/L ≤ 1, and L = 1.86393 is the duct length. A noise source is imposed at  z′ = 0, henceforth referred to as the source plane. This is where the fan would be located in the actual engine geometry. The plane  z = L corresponds to the fore end of the engine and is referred to as the inlet plane.
For the reference quantities in this model, choose the duct radius, the mean-flow speed of sound, and the mean-flow density at the source plane. Hence, all three of these quantities take the value 1.
To facilitate the COMSOL Multiphysics modeling, add a set of auxiliary domains to the geometry:
•
A cylindrical domain — adjoined at the inlet plane and extending to the terminal plane, z = 2.86393 — extends the modeling domain into a region where you can consider the mean flow as being uniform. This allows you to impose the simple boundary condition of a constant velocity potential and a vanishing tangential velocity for the background flow at the terminal plane.
•
PML domains, adjoined at the source and terminal planes, allow you to conveniently implement nonreflecting boundary conditions for the aeroacoustic field. At the source plane, the PML domain is split into three annular sections with the innermost and outermost sections damping both in the axial and radial directions, while the central one is damping only in the axial direction. For more information about PMLs, see the COMSOL Multiphysics Reference Manual.
The remaining boundary conditions for the mean flow consist of a natural boundary condition specifying the mass-flow rate through the source plane via the normal velocity and the density; slip conditions (vanishing tangential velocity) at the duct wall and at the spinner; and axial symmetry at r = 0.
For the aeroacoustic field, the model considers two different boundary conditions at the duct wall:
•
Sound hard — the normal component of the acoustic particle velocity vanishes at the boundary.
•
Impedance — the normal component of the acoustic particle velocity is related to the particle displacement through the equation
where Z is the impedance. This boundary condition, first derived by Myers (Ref. 2), was later recast in a weak form by Eversman (Ref. 3); it is this weak version, which is directly suitable for finite element modeling, that is implemented in the Acoustics Module’s Linearized Potential Flow, Frequency Domain interface. The impedance boundary condition represents a lined duct wall. In this model, following Ref. 1, the impedance is taken to be Z = 2 −  i.
The spinner, in contrast, is always assumed to be acoustically hard.
This study examines two cases for the mean-flow normal velocity component at the source plane, Vz, which (owing to the choice of reference speed) alternatively can be referred to as the source-plane axial Mach number M = − 0.5, approximately representative of a passenger aircraft at cruising speed, and M =  0.
The dimensionless angular frequency (nondimensionalized through division by
R∞/c∞) is ω = 16, and the azimuthal mode number is m = 10. If you want to obtain a deeper understanding of the duct’s aeroacoustic characteristics, you can, of course, perform a systematic exploration of parameter space by varying these quantities independently.
Results and Discussion
The Mean-Flow Field
For the nontrivial case of a source-plane axial Mach number of M = −0.5, the resulting mean-flow field appears in Figure 2. Note that the velocity potential is uniform well beyond the terminal plane, thus justifying the boundary condition imposed there. Furthermore, as could be expected, deviations from the mean density value appear primarily near the nonuniformities of the duct geometry, such as at the tip of the spinner.
As a complement, a more quantitative picture of the variations of the mean-flow velocity and density profiles along the axial direction appear in the cross-section plots in Figure 3.
Figure 2: Mean-flow velocity potential and density for source-plane Mach number M = −0.5.
Figure 3: Mean-flow cross section plot at a sample radius of  0.8.
The Noise Source
With the solution for the mean-flow field at hand, it is possible to calculate the corresponding eigenmodes for the acoustic field at the source plane. Figure 4 shows the resulting velocity-potential profile for the lowest mode. This is the boundary mode used as the source of the acoustic noise field in the duct for the case M = −0.5.
Figure 4: The first axial boundary mode at the source plane (z = 0) for the case of a background flow with Mach number M = −0.5.
The Aeroacoustic Field
The pressure fields for the case without a background mean flow, shown in Figure 5, very closely match those for the corresponding finite element model (FEM) solutions presented in Figure 6 of  Ref. 1. Similarly, the results for the attenuation between the source and inlet planes in the lined-wall case are in good agreement: 50.6 dB for the COMSOL Multiphysics solution versus 51.6 dB for the FEM solution in Ref. 1.
Figure 5: Acoustic pressure field for the cases of hard (top) and lined (bottom) duct wall with no mean flow and at circumferential mode number m = 10 and angular frequency ω = 16.
Turning to the case with a mean flow, the pressure field for the hard-wall case in the upper image of Figure 6 closely resembles the FEM solution obtained by Rienstra and Eversman in Ref. 1. For the lined-wall case in the lower image, although the agreement is still quite good, you can note some differences, especially near the source plane. This observation extends to the attenuation, for which the calculated value of 25.2 dB differs slightly more from the value of 27.2 dB obtained in Ref. 1.
However, these discrepancies have a natural explanation: the source mode in the COMSOL Multiphysics calculation was derived for the case of a hard duct wall, whereas Rienstra and Eversman used a noise source adapted to the acoustic lining. The lowest mode for the lined-wall case is a linear combination of the two forward-propagating hard-wall modes. Thus, the noise source term used to obtain the FEM solution visualized in the lower plot of Figure 6 is not optimally adapted to the duct, and it is consequently not maximally attenuated.
Figure 6: Acoustic pressure distribution for the cases of hard (top) and lined (bottom) duct wall with mean flow (M = −0.5) and at circumferential mode number m = 10 and angular frequency ω = 16.
Notes About the COMSOL Implementation
The model involves three physics interfaces, the last of which is used twice:
•
Compressible Potential Flow (cpf) — for modeling the background mean-flow velocity field as a potential flow (a lossless and irrotational flow).
•
Linearized Potential Flow, Boundary Mode (aebm) — for calculating the boundary eigenmode to be used as the source of the acoustic noise in the background mean-flow.
•
Linearized Potential Flow, Frequency Domain (ae, ae2) — for modeling the time-harmonic acoustic field above and below the source plane.
After an initial modeling stage — consisting of creating the geometry and the mesh, then defining parameters, variables, and component couplings — you proceed with three consecutive stages corresponding to the items in the list above.
As explained in the Model Definition section, this model uses nondimensional variables obtained by dividing each variable by a suitable reference quantity of the same dimension. The reference length is the duct radius at the source plane (which is why it has the value 1). The mean-flow density and speed of sound at the source plane (z = 0) complete the set of reference variables.
References
1. S.W. Rienstra and W. Eversman, “A Numerical Comparison Between the Multiple-Scales and Finite-Element Solution for Sound Propagation in Lined Flow Ducts,” J. Fluid Mech., vol. 437, pp. 367–384, 2001.
2. M.K. Myers, “On the Acoustic Boundary Condition in the Presence of Flow,” J. Sound Vib., vol. 71, pp. 429–434, 1980.
3. W. Eversman, “The Boundary Condition at an Impedance Wall in a Non-Uniform Duct with Potential Mean Flow,” J. Sound Vib., vol. 246, pp. 63–69, 2001. Errata: ibid,  vol. 258, pp. 791–792, 2002.
Application Library path: Acoustics_Module/Aeroacoustics_and_Noise/flow_duct
Modeling Instructions
From the File menu, choose New.
New
In the New window, click  Model Wizard.
Model Wizard
1
In the Model Wizard window, click  2D Axisymmetric.
2
In the Select Physics tree, select Acoustics>Aeroacoustics>Compressible Potential Flow (cpf).
3
Click Add.
4
In the Select Physics tree, select Acoustics>Aeroacoustics>Linearized Potential Flow, Boundary Mode (aebm).
5
Click Add.
6
In the Velocity potential text field, type phi_b.
7
In the Select Physics tree, select Acoustics>Aeroacoustics>Linearized Potential Flow, Frequency Domain (ae).
8
Click Add twice.
9
Click  Study.
10
In the Select Study tree, select Preset Studies for Some Physics Interfaces>Stationary.
11
Click  Done.
Root
1
In the Model Builder window, click the root node.
2
In the root node’s Settings window, locate the Unit System section.
3
From the Unit system list, choose None.
This setting turns off all unit support in the model.
Global Definitions
Parameters 1
Load the parameters from a file. They define model and physical properties including the liner impedance.
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click  Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file flow_duct_parameters.txt.
Geometry 1
First import the duct geometry, which is supplied in the form of an MPHBIN-file.
Import 1 (imp1)
1
In the Home toolbar, click  Import.
2
In the Settings window for Import, locate the Import section.
3
Click  Browse.
4
Browse to the model’s Application Libraries folder and double-click the file flow_duct.mphbin.
5
Click  Import.
Next, add the auxiliary cylindrical domain between the inlet plane at z = 1.86393 and the terminal plane at z = 2.86393, including a PML layer.
Rectangle 1 (r1)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 0.91705.
4
In the Height text field, type 1.2.
5
Locate the Position section. In the z text field, type zi.
6
Click to expand the Layers section. Clear the Layers on bottom check box.
7
Select the Layers on top check box.
8
In the table, enter the following settings:
Layer name
Thickness
Layer 1
0.2
9
Click  Build Selected.
10
Click the  Zoom Extents button in the Graphics toolbar.
Finally, attach the cylindrical PML domain at the outlet. This domain is divided into three as the PML here will be damping both in the axial and radial directions.
Rectangle 2 (r2)
1
In the Geometry toolbar, click  Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type 1.
4
In the Height text field, type 0.2.
5
Locate the Position section. In the r text field, type 0.2.
6
In the z text field, type -0.2.
7
Click  Build Selected.
Thicken 1 (thi1)
1
In the Geometry toolbar, click  Conversions and choose Thicken.
2
In the Settings window for Thicken, locate the Input section.
3
From the Geometric entity level list, choose Boundary.
4
On the object imp1, select Boundary 34 only.
5
Select the Keep input objects check box.
6
Locate the Options section. From the Offset list, choose Asymmetric.
7
In the Upside thickness text field, type 0.2.
8
Click  Build All Objects.
Form Union (fin)
1
In the Geometry toolbar, click  Build All.
2
Click the  Zoom Extents button in the Graphics toolbar.
The model geometry is now complete. The axisymmetric model geometry including duct domain and auxiliary domains.
Mesh 1
Create a user-defined mapped mesh that is sufficiently fine to resolve the small-scale acoustic perturbations by following the instructions below.
Mapped 1
In the Mesh toolbar, click  Mapped.
Distribution 1
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundary 1 only.
This is the duct domain’s boundary along the symmetry axis.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 39.
Distribution 2
1
In the Model Builder window, right-click Mapped 1 and choose Distribution.
2
Select Boundary 3 only.
This is the symmetry-axis boundary segment for the auxiliary domain above the duct.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 60.
Distribution 3
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundaries 6 and 43 only.
These are the source-plane and terminal-plane boundaries. Note that you can make the selection by clicking the Paste Selection button and typing the indices in the dialog box that opens.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 40.
Distribution 4
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundaries 5, 19, 20, 96, and 97 only.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 18.
Distribution 5
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundary 2 only.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 1.
Distribution 6
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundaries 8–18, 22–39, and 66–94 only.
You can do this most easily by copying the text 8-18, 22-39, 66-94 and then clicking in the Selection box and pressing Ctrl+V or by using the Paste Selection dialog box.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 3.
Distribution 7
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundaries 40 and 95 only.
Distribution 8
1
Right-click Mapped 1 and choose Distribution.
2
Select Boundaries 44–59 and 62–65 only.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 2.
5
Click  Build All.
The finished mesh should look like that in the figure below.
Definitions
Variables 1
1
In the Home toolbar, click  Variables and choose Local Variables.
2
In the Settings window for Variables, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domains 1 and 2 only.
5
Locate the Variables section. In the table, enter the following settings:
Name
Expression
Description
Mz
-cpf.Vz
Axial Mach number
Next, define an expression for the source mode’s intensity component normal to the source boundary.
Variables 2
1
In the Home toolbar, click  Variables and choose Local Variables.
2
In the Settings window for Variables, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundary 43 only.
5
Locate the Variables section. In the table, enter the following settings:
Name
Expression
Description
Iz_src
A^2*0.5*real((aebm.p/cpf.rhoref+aebm.Vr*aebm.vr-aebm.Vz*aebm.ikz*phi_b)*conj(rho*aebm.Vz-cpf.rhoref*aebm.ikz*phi_b))
Source mode intensity, normal component
Proceed by defining nonlocal integration couplings for the source and inlet planes for use in computing the attenuation.
Integration 1 (intop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_src in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
Select Boundary 43 only.
Integration 2 (intop2)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, type intop_inl in the Operator name text field.
3
Locate the Source Selection section. From the Geometric entity level list, choose Boundary.
4
Select Boundary 4 only.
Using these couplings, define variables for the power through the source and inlet planes.
Variables 3
1
In the Definitions toolbar, click  Local Variables.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Description
W_src
intop_src(Iz_src)
Power through source plane
W_inl
intop_inl(ae.Iz)
Power through inlet plane
The integral is automatically performed in the full azimuthal direction, because of the option selected in the integration coupling.
Because the variables you just defined cannot be evaluated for the same solution datasets, it is not possible to define a variable for the attenuation. Instead, create an analytic function that returns the attenuation when supplied with two power values.
Attenuation
1
In the Definitions toolbar, click  Analytic.
2
In the Settings window for Analytic, type Attenuation in the Label text field.
3
In the Function name text field, type dw.
4
Locate the Definition section. In the Expression text field, type 10*log10(w_src/w_in).
5
In the Arguments text field, type w_src, w_in.
The Background Flow and the Source
In the following modeling steps you derive the stationary background as well as the acoustic source at the duct entrance. Both are used when modeling the time-harmonic acoustic perturbations that you will set up following this.
You calculate the stationary flow field using the Compressible Potential Flow interface defined on the duct geometry (Domain 1) and on the auxiliary region (Domain 2) appended at the inlet plane (z = 1.86393). Impose a mass-flow boundary condition at the source plane and a normal-flow condition at the terminal plane (z = 2.86393). The duct wall and the spinner are both impervious to the flow.
As the source generating the acoustic field in the duct, use a single boundary mode imposed at z = 0. More specifically, take this mode to be the lowest propagating axial mode in the duct computed in the background flow field from the previous stage of the modeling process. The subsequent instructions demonstrate how to derive this boundary mode.
Proceed with setting up the background flow physics and couple it to the mode analysis model. Then solve everything coupled for two values of the Mach number (M = 0 and M = -0.5). The solution datasets will include both background flow and source data.
Compressible Potential Flow (cpf)
1
In the Model Builder window, under Component 1 (comp1) click Compressible Potential Flow (cpf).
2
Select Domains 1–3 only.
3
In the Settings window for Compressible Potential Flow, locate the Reference Values section.
4
In the pref text field, type cpf.rhoref^gamma/gamma.
5
In the ρref text field, type rho0.
6
In the vref text field, type M.
Compressible Potential Flow Model 1
1
In the Model Builder window, under Component 1 (comp1)>Compressible Potential Flow (cpf) click Compressible Potential Flow Model 1.
2
In the Settings window for Compressible Potential Flow Model, locate the Compressible Potential Flow Model section.
3
From the γ list, choose User defined. In the associated text field, type gamma.
Normal Flow 1
1
In the Physics toolbar, click  Boundaries and choose Normal Flow.
2
Select Boundary 7 only.
Mass Flow 1
1
In the Physics toolbar, click  Boundaries and choose Mass Flow.
2
Select Boundary 43 only.
Now set up Linearized Potential Flow, Boundary Mode physics for the boundary mode source calculation.
Linearized Potential Flow, Boundary Mode (aebm)
1
In the Model Builder window, under Component 1 (comp1) click Linearized Potential Flow, Boundary Mode (aebm).
2
In the Settings window for Linearized Potential Flow, Boundary Mode, locate the Boundary Selection section.
3
Click  Clear Selection.
4
Select Boundary 43 only.
5
Locate the Linearized Potential Flow Equation Settings section. In the m text field, type m.
Linearized Potential Flow Model 1
The following settings couple the aeroacoustics boundary mode to the background flow:
1
In the Model Builder window, under Component 1 (comp1)>Linearized Potential Flow, Boundary Mode (aebm) click Linearized Potential Flow Model 1.
2
In the Settings window for Linearized Potential Flow Model, locate the Linearized Potential Flow Model section.
3
From the ρ0 list, choose Density (cpf).
4
From the c0 list, choose Speed of sound (cpf/cpf1).
5
Specify the V vector as
cpf.Vr
r
cpf.Vz
z
6
In the Model Builder window, collapse the Linearized Potential Flow, Boundary Mode (aebm) node.
Study 1 - Background and Source
Set up the solver. Step 1 solves the stationary background field and Step 2 is the boundary mode analysis. The solution of the stationary step (the background flow) is automatically used in the mode analysis step.
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, type Study 1 - Background and Source in the Label text field.
Mode Analysis
1
In the Study toolbar, click  Study Steps and choose Other>Mode Analysis.
2
In the Settings window for Mode Analysis, locate the Study Settings section.
3
From the Transform list, choose Out-of-plane wave number.
4
In the Mode analysis frequency text field, type f.
5
Select the Desired number of modes check box.
6
In the associated text field, type 1.
7
From the Mode search method around shift list, choose Larger real part.
Parametric Sweep
1
In the Study toolbar, click  Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click  Add.
4
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
M (Mean flow Mach number)
0 -0.5
 
5
In the Study toolbar, click  Compute.
Results
Mean Flow Velocity, 3D (cpf)
The second default plot group is a 225° revolution plot of the velocity potential (of the first plot group).
In the plot you can also inspect the value of the out-of-plane wave number. Setting up the solver you only looked for the first propagating mode for each value of the Mach number. For M = 0 you have 10.84 and for M = -0.5 you have 5.778. The strong background flow has shifted the wave number.
NOTE: If you want to investigate more modes you can change the settings in the Mode Analysis study step. Set the desired number of modes, for example 12, and then set the search to Closest in absolute value. Solve again. Now, inspecting the Out-of-plane wave number list (for M = -0.5) you will find four solutions with a purely real wave number, three of them positive and one negative. In other words, there are four propagating waves, three of which propagate in the positive z direction and one in the opposite direction. The strong background flow has shifted the wave numbers, which in the absence of a mean flow would be symmetrically distributed around zero (if you select M = 0). If you had set these options you would have need to select the correct out-of-plane wave number in subsequent actions. Now you only have one wave number, the forward propagating one, for each M value.
To reproduce the plot shown in Figure 2 create a new 2D plot group.
Stationary: rho and Phi
1
In the Home toolbar, click  Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Stationary: rho and Phi in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Background and Source/Parametric Solutions 1 (sol3).
Surface 1
1
Right-click Stationary: rho and Phi and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type rho.
Contour 1
1
In the Model Builder window, right-click Stationary: rho and Phi and choose Contour.
2
In the Stationary: rho and Phi toolbar, click  Plot.
Compare the result with Figure 2.
Proceed with creating the figures in Figure 3 and Figure 4. First create a new dataset to get a detailed view of the density and velocity profiles along the length of the duct.
Cut Line 2D 1
1
In the Results toolbar, click  Cut Line 2D.
2
In the Settings window for Cut Line 2D, locate the Line Data section.
3
In row Point 1, set R to 0.8.
4
In row Point 2, set R to 0.8 and z to 1.86393.
5
Locate the Data section. From the Dataset list, choose Study 1 - Background and Source/Parametric Solutions 1 (sol3).
6
Click  Plot.
7
Click the  Zoom Extents button in the Graphics toolbar.
Stationary: rho and Mz
1
In the Results toolbar, click  1D Plot Group.
2
In the Settings window for 1D Plot Group, type Stationary: rho and Mz in the Label text field.
3
Locate the Data section. From the Dataset list, choose Cut Line 2D 1.
4
From the Parameter selection (M) list, choose From list.
5
In the Parameter values (M) list, select -0.5.
6
From the Out-of-plane wave number selection list, choose First.
7
Locate the Legend section. From the Position list, choose Middle left.
Line Graph 1
1
Right-click Stationary: rho and Mz and choose Line Graph.
2
In the Settings window for Line Graph, locate the y-Axis Data section.
3
In the Expression text field, type rho.
4
Locate the x-Axis Data section. From the Parameter list, choose Expression.
5
In the Expression text field, type z.
6
Click to expand the Legends section. From the Legends list, choose Manual.
7
Select the Show legends check box.
8
In the table, enter the following settings:
Legends
Density
Line Graph 2
1
Right-click Line Graph 1 and choose Duplicate.
2
In the Settings window for Line Graph, locate the y-Axis Data section.
3
In the Expression text field, type Mz.
4
Locate the Legends section. In the table, enter the following settings:
Legends
Axial Mach Number
5
In the Stationary: rho and Mz toolbar, click  Plot.
The resulting plot should closely resemble that in Figure 3.
Boundary Mode Potential: phi_b
1
In the Home toolbar, click  Add Plot Group and choose 1D Plot Group.
2
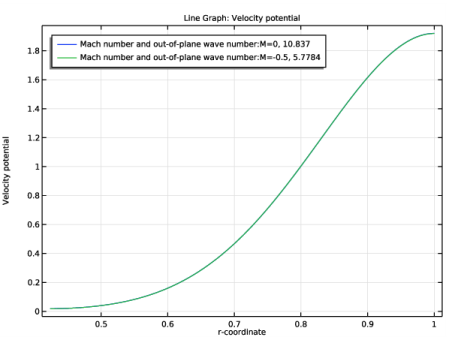
In the Settings window for 1D Plot Group, type Boundary Mode Potential: phi_b in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Background and Source/Parametric Solutions 1 (sol3).
4
From the Out-of-plane wave number selection list, choose First.
5
Locate the Legend section. From the Position list, choose Upper left.
Line Graph 1
1
Right-click Boundary Mode Potential: phi_b and choose Line Graph.
2
In the Settings window for Line Graph, locate the Selection section.
3
Click to select the  Activate Selection toggle button.
4
Select Boundary 43 only.
5
Locate the y-Axis Data section. In the Expression text field, type phi_b.
6
Locate the Legends section. Select the Show legends check box.
7
Find the Prefix and suffix subsection. In the Prefix text field, type Mach number and out-of-plane wave number: .
8
Locate the x-Axis Data section. From the Parameter list, choose Expression.
9
In the Expression text field, type r.
10
In the Boundary Mode Potential: phi_b toolbar, click  Plot.
The resulting plot of the desired boundary modes should closely resemble that in Figure 4. Note that the shapes of the two seem identical. Here the real part is plotted. Change the plot parameter to imag(phi_p) and you will see a difference.
The Acoustic Field
Equipped with the solution derived in the previous stage, you can now go on to simulate the acoustic field. Model the noise source through judicious choices of boundary conditions at the source plane (z = 0) for the two Linearized Potential Flow, Frequency Domain interfaces. Furthermore, implement nonreflecting boundary conditions at both ends of the duct geometry by using the auxiliary PML domains that you added to the model earlier in the geometry creation steps.
Here are the detailed instructions for the procedure.
Definitions
Also, create a nonlocal maximum coupling for the duct domain and use it to define a normalized absolute pressure variable.
Maximum 1 (maxop1)
1
In the Definitions toolbar, click  Nonlocal Couplings and choose Maximum.
2
Select Domain 1 only.
Variables 1
1
In the Model Builder window, click Variables 1.
2
In the Settings window for Variables, locate the Variables section.
3
In the table, enter the following settings:
Name
Expression
Description
pabsn
abs(ae.p)/comp1.maxop1(ae.p)
Normalized pressure
Perfectly Matched Layer 1 (pml1)
1
In the Definitions toolbar, click  Perfectly Matched Layer.
2
Select Domain 3 only.
3
In the Settings window for Perfectly Matched Layer, locate the Geometry section.
4
From the Type list, choose Cylindrical.
5
Locate the Scaling section. From the Typical wavelength from list, choose User defined.
6
In the Typical wavelength text field, type ae.c0/f.
Perfectly Matched Layer 2 (pml2)
1
Right-click Perfectly Matched Layer 1 (pml1) and choose Duplicate.
2
In the Settings window for Perfectly Matched Layer, locate the Domain Selection section.
3
Click  Clear Selection.
4
Select Domains 4–6 only.
5
Locate the Scaling section. In the Typical wavelength text field, type ae2.c0/f.
Linearized Potential Flow, Frequency Domain (ae)
1
In the Model Builder window, under Component 1 (comp1) click Linearized Potential Flow, Frequency Domain (ae).
2
Select Domains 1–3 only.
3
In the Settings window for Linearized Potential Flow, Frequency Domain, click to expand the Equation section.
4
Locate the Linearized Potential Flow Equation Settings section. In the m text field, type m.
Couple the mean-flow field to the linearized potential flow (LPF) model by using the dedicated Multiphysics coupling. Verify that the correct physics are coupled. The multiphysic coupling is not used for the second LPF physics. The latter represents a truncation domain with constant flow conditions.
Multiphysics
Background Potential Flow Coupling 1 (pfc1)
In the Physics toolbar, click  Multiphysics Couplings and choose Global>Background Potential Flow Coupling.
Linearized Potential Flow, Frequency Domain (ae)
Normal Mass Flow 1
1
In the Physics toolbar, click  Boundaries and choose Normal Mass Flow.
2
Select Boundary 43 only.
3
In the Settings window for Normal Mass Flow, locate the Normal Mass Flow section.
4
In the mn text field, type rho*(-aebm.ikz*A*phi_b).
Impedance 1
1
In the Physics toolbar, click  Boundaries and choose Impedance.
2
Select Boundaries 44–59 and 62–95 only.
3
In the Settings window for Impedance, locate the Impedance section.
4
In the Zi text field, type Zw/flc2hs(z/zi,b).
The reason behind using the smoothed Heaviside function flc2hs is to make the impedance a continuous (albeit abruptly changing) function across the interfaces between regions with and without an acoustic lining. This is a condition required for the equivalence of Myers’s original impedance boundary condition and its weak reformulation due to Eversman used here to hold (see Ref. 3).
Impedance 2
1
In the Physics toolbar, click  Boundaries and choose Impedance.
2
Select Boundaries 60 and 61 only.
3
In the Settings window for Impedance, locate the Impedance section.
4
In the Zi text field, type Zw.
The second linearized potential flow interface is used to set up an open domain at the outlet. Since this interface has a different dependent variable (phi2), it allows to set up a port-like condition at the outlet with a discontinuous dependent variable (only the scattered field is absorbed).
Linearized Potential Flow, Frequency Domain 2 (ae2)
1
In the Model Builder window, under Component 1 (comp1) click Linearized Potential Flow, Frequency Domain 2 (ae2).
2
Select Domains 4–6 only.
3
In the Settings window for Linearized Potential Flow, Frequency Domain, locate the Linearized Potential Flow Equation Settings section.
4
In the m text field, type m.
Linearized Potential Flow Model 1
1
In the Model Builder window, under Component 1 (comp1)>Linearized Potential Flow, Frequency Domain 2 (ae2) click Linearized Potential Flow Model 1.
2
In the Settings window for Linearized Potential Flow Model, locate the Linearized Potential Flow Model section.
3
From the ρ0 list, choose User defined. In the associated text field, type rho0.
4
From the c0 list, choose User defined. In the associated text field, type C0.
5
Specify the V vector as
0
r
M
z
Linearized Potential Flow Model 2
1
Right-click Component 1 (comp1)>Linearized Potential Flow, Frequency Domain 2 (ae2)>Linearized Potential Flow Model 1 and choose Duplicate.
2
Select Domains 4 and 6 only.
3
In the Settings window for Linearized Potential Flow Model, locate the Linearized Potential Flow Model section.
4
Specify the V vector as
0
r
0
z
Velocity Potential 1
1
In the Physics toolbar, click  Boundaries and choose Velocity Potential.
The potential is set equal to only the scattered potential from the main domain, that is, the total potential phi minus the incident potential A*phi_b.
2
Select Boundary 43 only.
3
In the Settings window for Velocity Potential, locate the Velocity Potential section.
4
In the φ0 text field, type phi-A*phi_b.
Linearized Potential Flow, Frequency Domain 2 (ae2)
In the Model Builder window, collapse the Component 1 (comp1)>Linearized Potential Flow, Frequency Domain 2 (ae2) node.
Next compute the acoustic fields for the case with (M = -0.5) and without (M = 0) background flow as well as with and without the wall lining. Do this by adding four frequency domain studies, select the desired background flow solution, and enable or disable the impedance boundary condition using the Modify physics tree and variables for study step option in the solver step.
Add Study
1
In the Home toolbar, click  Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Compressible Potential Flow (cpf) and Linearized Potential Flow, Boundary Mode (aebm).
4
Find the Studies subsection. In the Select Study tree, select General Studies>Frequency Domain.
5
Click Add Study in the window toolbar.
6
In the Select Study tree, select Preset Studies for Some Physics Interfaces>Frequency Domain.
7
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Compressible Potential Flow (cpf) and Linearized Potential Flow, Boundary Mode (aebm).
8
Click Add Study in the window toolbar.
9
Find the Studies subsection. In the Select Study tree, select Preset Studies for Some Physics Interfaces>Frequency Domain.
10
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Compressible Potential Flow (cpf) and Linearized Potential Flow, Boundary Mode (aebm).
11
Click Add Study in the window toolbar.
12
Find the Studies subsection. In the Select Study tree, select Preset Studies for Some Physics Interfaces>Frequency Domain.
13
Find the Physics interfaces in study subsection. In the table, clear the Solve check boxes for Compressible Potential Flow (cpf) and Linearized Potential Flow, Boundary Mode (aebm).
14
Click Add Study in the window toolbar.
15
In the Home toolbar, click  Add Study to close the Add Study window.
Study 2 - Frequency Domain (M = 0, lined)
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
In the Label text field, type Study 2 - Frequency Domain (M = 0, lined).
Step 1: Frequency Domain
1
In the Model Builder window, under Study 2 - Frequency Domain (M = 0, lined) click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f.
4
Click to expand the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
5
From the Method list, choose Solution.
6
From the Study list, choose Study 1 - Background and Source, Mode Analysis.
7
From the Solution list, choose Parametric Solutions 1 (sol3).
8
From the Use list, choose M=0 (sol4).
9
In the Home toolbar, click  Compute.
Study 3 - Frequency Domain (M = -0.5, lined)
1
In the Model Builder window, click Study 3.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
In the Label text field, type Study 3 - Frequency Domain (M = -0.5, lined).
Step 1: Frequency Domain
1
In the Model Builder window, under Study 3 - Frequency Domain (M = -0.5, lined) click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f.
4
Locate the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
5
From the Method list, choose Solution.
6
From the Study list, choose Study 1 - Background and Source, Mode Analysis.
7
From the Solution list, choose Parametric Solutions 1 (sol3).
8
From the Use list, choose M=-0.5 (sol5).
9
In the Home toolbar, click  Compute.
Study 4 - Frequency Domain (M = 0, hard wall)
1
In the Model Builder window, click Study 4.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
In the Label text field, type Study 4 - Frequency Domain (M = 0, hard wall).
Step 1: Frequency Domain
1
In the Model Builder window, under Study 4 - Frequency Domain (M = 0, hard wall) click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f.
4
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
5
In the tree, select Component 1 (Comp1)>Linearized Potential Flow, Frequency Domain (Ae)>Impedance 1.
6
Click  Disable.
7
In the tree, select Component 1 (Comp1)>Linearized Potential Flow, Frequency Domain (Ae)>Impedance 2.
8
Click  Disable.
9
Locate the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
10
From the Method list, choose Solution.
11
From the Study list, choose Study 1 - Background and Source, Mode Analysis.
12
From the Solution list, choose Parametric Solutions 1 (sol3).
13
From the Use list, choose M=0 (sol4).
14
In the Home toolbar, click  Compute.
Study 5 - Frequency Domain (M = -0.5, hard wall)
1
In the Model Builder window, click Study 5.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
4
In the Label text field, type Study 5 - Frequency Domain (M = -0.5, hard wall).
Step 1: Frequency Domain
1
In the Model Builder window, under Study 5 - Frequency Domain (M = -0.5, hard wall) click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f.
4
Locate the Physics and Variables Selection section. Select the Modify model configuration for study step check box.
5
In the tree, select Component 1 (Comp1)>Linearized Potential Flow, Frequency Domain (Ae)>Impedance 1.
6
Click  Disable.
7
In the tree, select Component 1 (Comp1)>Linearized Potential Flow, Frequency Domain (Ae)>Impedance 2.
8
Click  Disable.
9
Locate the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
10
From the Method list, choose Solution.
11
From the Study list, choose Study 1 - Background and Source, Mode Analysis.
12
From the Solution list, choose Parametric Solutions 1 (sol3).
13
From the Use list, choose M=-0.5 (sol5).
14
In the Home toolbar, click  Compute.
Results
First, have a look at the mean flow velocity and add arrow to understand the flow direction. This is also the direction that defines the outlet and inlet of the model. You can also inspect the remaining default plots generated by the first study.
Arrow Surface 1
1
In the Model Builder window, right-click Mean Flow Velocity (cpf) and choose Arrow Surface.
2
In the Settings window for Arrow Surface, locate the Coloring and Style section.
3
From the Color list, choose Black.
4
In the Mean Flow Velocity (cpf) toolbar, click  Plot.
Pressure: M = 0, lined
Now, proceed to create the results depicted in Figure 5 and in Figure 6. Start by creating one plot and set it up, then simply duplicate the plot and select the correct dataset. After generating the plots proceed to calculating the attenuation of the system under Derived Values in the Results node.
1
In the Home toolbar, click  Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Pressure: M = 0, lined in the Label text field.
3
Click to expand the Title section. From the Title type list, choose Manual.
4
In the Title text area, type Normalized Pressure (M = 0, lined).
5
Clear the Parameter indicator text field.
6
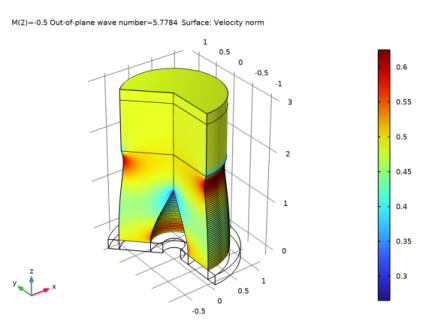
Locate the Data section. From the Dataset list, choose Study 2 - Frequency Domain (M = 0, lined)/Solution 6 (sol6).
Contour 1
1
Right-click Pressure: M = 0, lined and choose Contour.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type pabsn.
4
Locate the Levels section. From the Entry method list, choose Levels.
5
In the Levels text field, type 0.0001 0.001 0.01 0.02 0.04 0.06 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9.
6
Locate the Coloring and Style section. From the Contour type list, choose Filled.
7
From the Legend type list, choose Line.
8
Clear the Color legend check box.
Contour 2
1
In the Model Builder window, right-click Pressure: M = 0, lined and choose Contour.
2
In the Settings window for Contour, locate the Expression section.
3
In the Expression text field, type pabsn.
4
Locate the Levels section. From the Entry method list, choose Levels.
5
In the Levels text field, type 0.0001 0.001 0.01 0.02 0.04 0.06 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9.
6
Locate the Coloring and Style section. From the Coloring list, choose Uniform.
7
Clear the Color legend check box.
8
In the Pressure: M = 0, lined toolbar, click  Plot.
The plot does not look exactly like the one at the top of Figure 5, this is because only the solution inside the flow duct is of interest. Add selections to the datasets to restrict plotting to this domain.
Study 2 - Frequency Domain (M = 0, lined)/Solution 6 (sol6)
In the Model Builder window, under Results>Datasets click Study 2 - Frequency Domain (M = 0, lined)/Solution 6 (sol6).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 1 only.
Study 3 - Frequency Domain (M = -0.5, lined)/Solution 7 (sol7)
In the Model Builder window, under Results>Datasets click Study 3 - Frequency Domain (M = -0.5, lined)/Solution 7 (sol7).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 1 only.
Study 4 - Frequency Domain (M = 0, hard wall)/Solution 8 (sol8)
In the Model Builder window, under Results>Datasets click Study 4 - Frequency Domain (M = 0, hard wall)/Solution 8 (sol8).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 1 only.
Study 5 - Frequency Domain (M = -0.5, hard wall)/Solution 9 (sol9)
In the Model Builder window, under Results>Datasets click Study 5 - Frequency Domain (M = -0.5, hard wall)/Solution 9 (sol9).
Selection
1
In the Results toolbar, click  Attributes and choose Selection.
2
In the Settings window for Selection, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 1 only.
Pressure: M = 0, lined
1
In the Model Builder window, under Results click Pressure: M = 0, lined.
2
In the Pressure: M = 0, lined toolbar, click  Plot.
3
Click the  Zoom Extents button in the Graphics toolbar.
This should look like the lower plot in Figure 5.
Pressure: M = -0.5, lined
1
Right-click Pressure: M = 0, lined and choose Duplicate.
2
In the Settings window for 2D Plot Group, type Pressure: M = -0.5, lined in the Label text field.
3
Locate the Title section. In the Title text area, type Normalized Pressure (M = -0.5, lined).
4
Locate the Data section. From the Dataset list, choose Study 3 - Frequency Domain (M = -0.5, lined)/Solution 7 (sol7).
5
In the Pressure: M = -0.5, lined toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
This should look like the lower plot in Figure 6.
Pressure: M = 0, hard wall
1
Right-click Pressure: M = -0.5, lined and choose Duplicate.
2
In the Settings window for 2D Plot Group, type Pressure: M = 0, hard wall in the Label text field.
3
Locate the Title section. In the Title text area, type Normalized Pressure (M = 0, hard wall).
4
Locate the Data section. From the Dataset list, choose Study 4 - Frequency Domain (M = 0, hard wall)/Solution 8 (sol8).
5
In the Pressure: M = 0, hard wall toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
This should look like the upper plot in Figure 5.
Pressure: M = -0.5, hard wall
1
Right-click Pressure: M = 0, hard wall and choose Duplicate.
2
In the Settings window for 2D Plot Group, type Pressure: M = -0.5, hard wall in the Label text field.
3
Locate the Title section. In the Title text area, type Normalized Pressure (M = -0.5, hard wall).
4
Locate the Data section. From the Dataset list, choose Study 5 - Frequency Domain (M = -0.5, hard wall)/Solution 9 (sol9).
5
In the Pressure: M = -0.5, hard wall toolbar, click  Plot.
6
Click the  Zoom Extents button in the Graphics toolbar.
This should look like the upper plot in Figure 6.
Finally, calculate the attenuation. But first, determine the power at the source and the duct inlet. These numerical values are used to evaluate the attenuation using the attenuation function dw you have created.
Global Evaluation: W_src (M = 0)
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Global Evaluation: W_src (M = 0) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1 - Background and Source/Parametric Solutions 1 (sol3).
4
From the Parameter selection (M) list, choose First.
5
From the Out-of-plane wave number selection list, choose First.
6
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
W_src
 
Power through source plane
7
Click  Evaluate.
Global Evaluation: W_src (M = -0.5)
1
Right-click Global Evaluation: W_src (M = 0) and choose Duplicate.
2
In the Settings window for Global Evaluation, type Global Evaluation: W_src (M = -0.5) in the Label text field.
3
Locate the Data section. From the Parameter selection (M) list, choose Last.
4
Click the small triangle in the Settings window toolbar and choose New Table from the menu.
Global Evaluation: W_inl (M = 0, lined)
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Global Evaluation: W_inl (M = 0, lined) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 2 - Frequency Domain (M = 0, lined)/Solution 6 (sol6).
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
W_inl
 
Power through inlet plane
5
Click the small triangle in the Settings window toolbar and choose New Table from the menu.
Global Evaluation: W_inl (M = -0.5, lined)
1
Right-click Global Evaluation: W_inl (M = 0, lined) and choose Duplicate.
2
In the Settings window for Global Evaluation, type Global Evaluation: W_inl (M = -0.5, lined) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 3 - Frequency Domain (M = -0.5, lined)/Solution 7 (sol7).
4
Click the small triangle in the Settings window toolbar and choose New Table from the menu.
Global Evaluation: Attenuation (M = 0, lined)
1
In the Results toolbar, click  Global Evaluation.
2
In the Settings window for Global Evaluation, type Global Evaluation: Attenuation (M = 0, lined) in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 2 - Frequency Domain (M = 0, lined)/Solution 6 (sol6).
4
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
comp1.dw(0.02796, 2.43e-7)
 
Attenuation
5
Click  Evaluate.
The result should be approximately 50.6 dB, which is quite close to that in Ref. 1 (51.6 dB). The reason is that both use the same source mode as a result of the fact that there is a single forward-propagating mode in the flow-free case, thus making the two calculations directly comparable.
Global Evaluation: Attenuation (M = -0.5, lined)
1
Right-click Global Evaluation: Attenuation (M = 0, lined) and choose Duplicate.
2
In the Settings window for Global Evaluation, type Global Evaluation: Attenuation (M = -0.5, lined) in the Label text field.
3
Locate the Expressions section. In the table, enter the following settings:
Expression
Unit
Description
comp1.dw(9.5194e-3, 2.8650e-5)
 
Attenuation
4
Click the small triangle in the Settings window toolbar and choose New Table from the menu.
The result should now be roughly to 25.2 dB. Compare this result to the value of approximately 27 dB obtained for the corresponding quantity in Ref. 1. In contrast to that paper, the source mode used in these calculations was derived for the case of a hard duct wall, whereas the lowest mode for the lined-wall case would be a linear combination of the two forward-propagating hard-wall modes. For this reason, the noise source is not an eigenmode and is, consequently, not maximally attenuated.