
|
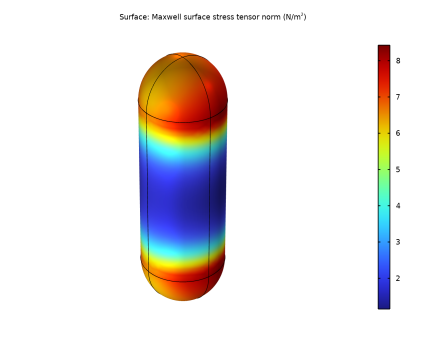
|
1
|
|
2
|
In the Select Physics tree, select AC/DC>Magnetic Fields, No Currents>Magnetic Fields, No Currents, Boundary Elements (mfncbe).
|
|
3
|
Click Add.
|
|
4
|
In the Select Physics tree, select AC/DC>Magnetic Fields, No Currents>Magnetic Fields, No Currents (mfnc).
|
|
5
|
Click Add.
|
|
6
|
In the Select Physics tree, select AC/DC>Magnetic Fields, No Currents>Magnetic Fields, No Currents, Boundary Elements (mfncbe).
|
|
7
|
Click Add.
|
|
8
|
Click
|
|
9
|
|
10
|
Click
|
|
1
|
|
2
|
Browse to the model’s Application Libraries folder and double-click the file force_calculation_01_introduction.mph.
|
|
3
|
In the Insert Sequence from File dialog box, select Geometry 1 (Magnetic Force Verification) in the Select geometry sequence to insert list.
|
|
4
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file force_calculation_b_mforce_parameters.txt.
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
In the Paste Selection dialog box, type 15, 16, 21, 22, 31, 34, 42, 43 in the Selection text field (that is, the boundaries comprising the pole fillets).
|
|
6
|
Click OK.
|
|
7
|
|
1
|
|
2
|
|
3
|
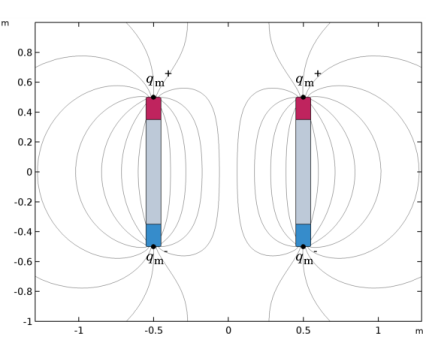
Select Domains 2–4 only (that is, both the magnetized rod, as well as the domain enclosing it).
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Magnetic Fields, No Currents, Boundary Elements (mfncbe).
|
|
2
|
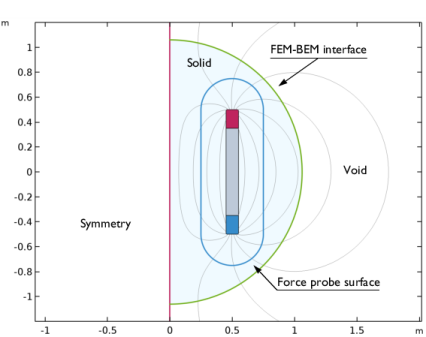
In the Settings window for Magnetic Fields, No Currents, Boundary Elements, click to expand the Symmetry section.
|
|
3
|
|
4
|
|
5
|
In the Show More Options dialog box, in the tree, select the check box for the node Physics>Advanced Physics Options.
|
|
6
|
Click OK.
|
|
7
|
In the Settings window for Magnetic Fields, No Currents, Boundary Elements, click to expand the Far-Field Approximation section.
|
|
8
|
|
9
|
Click to expand the Infinity Condition section. From the Infinity condition list, choose Zero magnetic scalar potential at infinity.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Constitutive Relation B-H section. From the Magnetization model list, choose Remanent flux density.
|
|
5
|
|
6
|
Specify the e vector as
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Constitutive Relation B-H section. From the Magnetization model list, choose Remanent flux density.
|
|
5
|
|
6
|
Specify the e vector as
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Magnetic Fields, No Currents, Boundary Elements 2 (mfncbe2).
|
|
2
|
In the Settings window for Magnetic Fields, No Currents, Boundary Elements, locate the Domain Selection section.
|
|
3
|
|
4
|
|
5
|
Locate the Infinity Condition section. From the Infinity condition list, choose Zero magnetic scalar potential at infinity.
|
|
1
|
In the Physics toolbar, click
|
|
2
|
In the Settings window for Magnetic Scalar-Scalar Potential Coupling, locate the Coupled Interfaces section.
|
|
3
|
From the Secondary interface (magnetic scalar potential) list, choose Magnetic Fields, No Currents, Boundary Elements 2 (mfncbe2).
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click
|
|
4
|
In the table, enter the following settings (make sure the parameter unit is cleared):
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
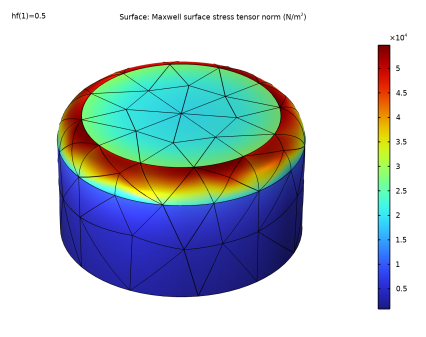
In the Settings window for 3D Plot Group, type Maxwell Surface Stress Tensor (BEM Rod) in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type sqrt(mfncbe.nTx_BEM_rod^2+mfncbe.nTy_BEM_rod^2+mfncbe.nTz_BEM_rod^2).
|
|
4
|
Select the Description check box.
|
|
5
|
In the associated text field, type Maxwell surface stress tensor norm.
|
|
6
|
|
7
|
|
1
|
In the Model Builder window, right-click Maxwell Surface Stress Tensor (BEM Rod) and choose Surface.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Select the Wireframe check box.
|
|
8
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Maxwell Surface Stress Tensor (BEM Probe) in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type sqrt(mfncbe.nTx_BEM_probe^2+mfncbe.nTy_BEM_probe^2+mfncbe.nTz_BEM_probe^2).
|
|
4
|
Select the Description check box.
|
|
5
|
In the associated text field, type Maxwell surface stress tensor norm.
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
Click
|
|
1
|
Go to the Table window.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Find the Physics interfaces in study and Multiphysics couplings in study subsections. In the tables, enter the following settings:
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
Click
|
|
4
|
In the table, enter the following settings (make sure the parameter unit is cleared):
|
|
1
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Maxwell Surface Stress Tensor (FEM Rod) in the Label text field.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Select the Description check box.
|
|
5
|
In the associated text field, type Maxwell surface stress tensor norm.
|
|
6
|
|
7
|
|
1
|
In the Model Builder window, right-click Maxwell Surface Stress Tensor (FEM Rod) and choose Surface.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Select the Wireframe check box.
|
|
8
|
|
1
|
|
2
|
In the Settings window for 3D Plot Group, type Maxwell Surface Stress Tensor (FEM Probe) in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type sqrt(mfnc.nTx_FEM_probe^2+mfnc.nTy_FEM_probe^2+mfnc.nTz_FEM_probe^2).
|
|
4
|
Select the Description check box.
|
|
5
|
In the associated text field, type Maxwell surface stress tensor norm.
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Expressions section. In the table, enter the following settings:
|
|
5
|
Click
|
|
1
|
Go to the Table window.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
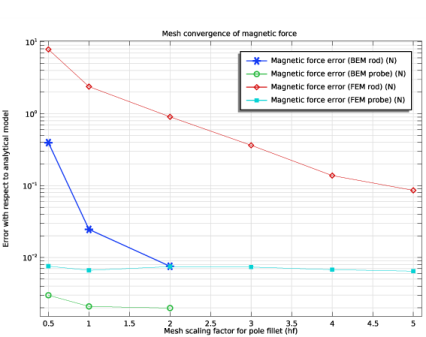
In the associated text field, type Mesh scaling factor for pole fillet (hf).
|
|
7
|
|
8
|
In the associated text field, type Error with respect to analytical model.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Coloring and Style section. Find the Line markers subsection. From the Marker list, choose Cycle.
|
|
5
|
|
6
|
|
7
|
|
8
|