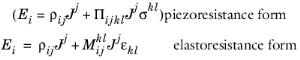The constitutive relations defined in Equation 6-2 relate the change in resistivity matrix (a rank 2 tensor) to the stress or strain matrix (also a rank 2 tensor). This means that the piezoresistivity tensor and the elastoresistance tensor are both rank 4 tensors. A formal tensor formulation of
Equation 6-1 therefore takes the form:
Here the Einstein summation convention is used. Note that this equation implies that Δρij=
Πijklσkl and
Δρij=
Mijklεkl. The tensors
Π and
M have a number of symmetry properties, that result from the fact that both
σ,
ε, and
Δρ are symmetric and can be represented in the following form:
As a result of this symmetry, it is possible to represent σ,
ε, and
Δρ as six component vectors. There are two conventions for ordering the components in these vectors and the Piezoresistivity interfaces all use the Voigt notation prevalent in the literature.
Where π and
m are now matrices related to the components of the corresponding
Π and
M tensors in the following manner:
Components of the Π and
M tensors that do not appear in these matrices are always equal to one of those that does appear as a result of symmetry constraints.
This is because the rank four tensors Π and
M lack one of the symmetry properties of the elasticity tensor (
Πijkl≠Πklij and
Mijkl≠Mklij see
Ref. 1 and
Ref. 2 for details). Finally the relationship between
π and
m is given by:
where D is the elasticity matrix (s=D
⋅e), which is defined in Voigt notation as: