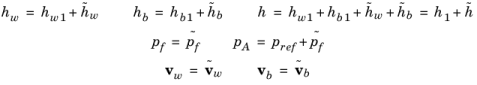
|
Since the frequency domain results do not depend on the variation in the displacement, the additional displacement setting has no effect on the solution in a frequency-domain problem (unless the velocity is computed from it by selecting Calculate from wall displacement or Calculate from base displacement in the wall and base velocity settings, respectively). This is reflected in the equations given above (and in the equation display in the physics interface) but can be nonintuitive, particularly when setting up a model that is coupled with a structural analysis. If the velocity of both the wall and the base is set to zero, then in the frequency domain there is no response.
|