In 2D geometries, the temperature is assumed to be constant in the out-of-plane direction (z direction with default spatial coordinate names). The equation for heat transfer in solids,
Equation 4-16, and in fluids,
Equation 4-18, are replaced by:
Here dz is the thickness of the domain in the out-of-plane direction. Here, the conductive heat flux,
q, becomes
In 1D axisymmetric geometries, the temperature is assumed to be constant in the out-of-plane direction (z direction with default spatial coordinate names) in addition to the axisymmetry (
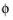
-coordinate with default spatial coordinate names). The equation for heat transfer in solids,
Equation 6-15 is replaced by
where dz is the thickness of the domain in the
z direction. The equation for heat transfer in fluids,
Equation 6-5, is replaced by
where Ac is the cross section of the domain in the plane perpendicular to the 1D geometry. The equation for heat transfer in fluids,
Equation 6-5, is replaced by
where q0, z is the heat flux density distributed along the cross section perimeter.