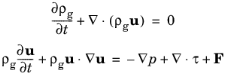See Theory for the Single-Phase Flow Interfaces and Theory for the Turbulent Flow Interfaces in the CFD Module User’s Guide for a description of the theory related to laminar and turbulent single-phase flow interfaces.

The density and viscosity of air might also vary due to temperature variations. See Theory for the Nonisothermal Flow and Conjugate Heat Transfer Interfaces for details on this other kind of dependency.

It also solves the equation for moisture transport in air, given in Equation 4-128 by

When the spatial and temporal variations of the vapor concentration induce significant variations of the moist air density, the moisture content variation is expressed through the transport of vapor mass fraction, ωv, defined as:

Surface reactions like evaporation and condensation result in a net moisture flux gw between the boundary and the domain. The resulting effective velocity at the boundary is the Stefan velocity uStefan, defined as

The Favre average of the vapor concentration cv is defined by

This flux is modeled using a gradient based assumption, where the additional transport is related to the turbulent viscosity νT through the turbulent Schmidt number ScT. The turbulent diffusivity DT is defined by

By analogy with turbulent heat transfer, the turbulent Schmidt number ScT is given by (Ref. 29)

where the Schmidt number at infinity is ScT∞ = 0.85 and the Schmidt number is defined as

where ν is the kinematic viscosity.

Analogous to the single-phase flow wall functions (see Wall Functions described for the Wall boundary condition), there is a theoretical gap between the solid wall and the computational domain for the fluid and relative humidity fields. This gap is often ignored when the computational geometry is drawn.

Assuming that the turbulent heat and moisture transfer in the near-wall region are analogous, the same type of wall functions used for the temperature (Ref. 31) is also applicable for the moisture transport. The moisture transfer wall function is formulated as a function of the turbulent Schmidt number, instead of the corresponding Prandtl number.

The moisture flux at the lift-off position between the air with vapor mass fraction ωv,a and a wall with vapor mass fraction ωv,w, is:

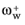
where uτ is the friction velocity, and is the dimensionless mass fraction given by (Ref. 31):

where κ is the von Karman constant equal to 0.41, Cμ is a turbulence modeling constant, and k is the turbulent kinetic energy.

The distance between the computational fluid domain and the wall, δw, is always hw/2 for automatic wall treatment where hw is the height of the mesh cell adjacent to the wall. hw/2 is almost always very small compared to any geometrical quantity of interest, at least if a boundary layer mesh is used. For wall function, δw is at least hw/2 and can be bigger if necessary to keep δw+ higher than 11.06. The computational results should be checked so that the distance between the computational fluid domain and the wall, δw, is everywhere small compared to any geometrical quantity of interest. The distance δw is available for evaluation on boundaries.