Add a Block Navier-Stokes node () under an Iterative solver node as an efficient preconditioner for the incompressible Navier–Stokes equations in the transient regime. This preconditioner is based on a block factorization of the Jacobian matrix problem coming from the Newton–Krylov approach to solve the time-and-space discretization of the incompressible Navier–Stokes equations. The Pressure Solver and Velocity Solver subnodes are always available for specifying general preconditioners for the pressure block and the velocity block, respectively.

In the Number of iterations field, enter the desired number of iterations (default: 1). When the convergence rate is poor, using a larger number of iterations can be a more efficient alternative compared to spend more efforts in either the velocity or pressure solver.

From the Schur complement approximation list, choose one of the following options:

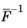
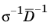
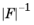
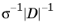
The Schur complement approximation component H is then computed as diag(F)−1, , , , and , respectively, where the overline notation is used for row summation (also called lumping) and the vertical bar notation is used for absolute row summation. F = σD + K in the COMSOL Multiphysics formulation with implicit time stepping. In that equation, F is a convection-diffusion-like operator, D is the velocity mass matrix, and K is the “stiffness matrix” from the convection and dissipation (including optional stabilization). σ is a factor that is proportional to the inverse time step.

For practical large-scale computations, use of the exact Schur complement is not feasible. Instead an approximation is used based on , where H is diagonal. The Schur matrix S is then approximated as

where 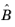is the divergence operator matrix, BT is the gradient operator matrix, and C is an operator that stabilizes the finite element discretization.

For each new assembly of the Jacobian matrix, the building blocks are updated, and the subsequent solver gets their corresponding updates. For certain problems — for example, formulations that do not require stabilization — the off-diagonal blocks are constant. For such formulations, and also for problems where the stabilization effect is small, a small performance benefit can be obtained by selecting the Reuse off-diagonal matrix blocks check box.

Enter a value between 0 and 2 in the Pressure update relaxation factor field (default: 0.95). See below for more information.

Under Velocity variables, click to add velocity variables, typically a velocity field from a fluid-flow interface.

Under Pressure variables, click to add pressure variables, typically a pressure field from a fluid-flow interface.

The Velocity variables and Pressure variables settings determine how the blocks are defined from the total Jacobian matrix. In cases where there are more variables than what is included in these settings solved for by the parent linear solver, the preconditioner will act like a hybrid preconditioner and only apply its action on the equations (residual) for the velocity and pressure variables. If you want updates for other variables, add another preconditioner and enable hybridization for them. Also, if the Navier–Stokes equations are formulated with other auxiliary equations that are of saddle-point type (for example, ODE variables for fully developed inlet boundary conditions), the corresponding variables should be added to the Pressure variables.

Each iteration j of the preconditioner applies the following operations and updates:

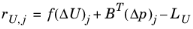
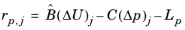
In the equations above, ω is the Pressure update relaxation factor and , . The Number of iterations controls how many of these iterations are performed. When the preconditioner is used with one iteration, an optimal value for the Pressure update relaxation factor should be around 0.9. When the preconditioner is used with two iterations a relaxation around 0.4–0.5 is often needed for good performance.

The operations 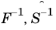are performed by the Velocity Solver and Pressure Solver subnodes, respectively. Those solvers can be chosen in the user interface. Algebraic multigrid solvers can be used. One of the benefits of the Block Navier-Stokes preconditioner is that standard SOR or SOR Line smoothers can be used for these multigrid solvers. Geometric multigrid is not supported.

Use the settings in the Hybridization section to set up a hybrid preconditioner where the direct preconditioner is active for some dependent variables. See Hybrid Preconditioners for more information.