The purpose of the Modal Solver is to speed up certain simulations by performing a model reduction using eigenpairs, making use of the solution to an eigenvalue or eigenfrequency problem to construct a basis using eigenvectors corresponding to the dominant dynamics. That is, the solution of the underlying system of equations is approximated by a linear combination of parametric or time-dependent coefficients and a few dominant eigenvectors.

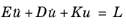where E is the mass matrix, D is the damping matrix, K is the stiffness matrix, and L is the load vector. Either E or D can be identically zero. The modal solver algorithm requires that a few eigenvectors have been computed. If you form a matrix Φ whose columns are m computed eigenvectors, and all appearing Dirichlet boundary conditions are homogeneous, then an approximation um of the solution u can be written as

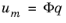where q is a small vector of unknown coefficients. Replacing u in Equation 20-10 by um and premultiplying by ΦH yield

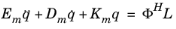The damping matrix D may be present when performing the eigenvalue analysis. It is, however, possible to add additional damping by providing damping ratios per mode (or one ratio for all modes). If λi denotes the ith eigenvalue and ξi the associated damping ratio, then

is added to the ith diagonal entry of the reduced damping matrix in Equation 20-12. If E and K are real and symmetric positive definite, D = 0, and Em and Km are diagonal, then ξi can be interpreted as the fraction of critical damping in the ith mode.

The Modal Solver (using a Time Dependent, Modal study step) can export matrices and the right-hand side for use in further simulations.

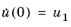
For time-dependent studies, the load L is assumed to be of the form l(t)L0, where L0 is constant, and l(t) is the given load factor. Further, the projection matrix Φ is possibly appended with one or two columns such that the initial values u(0) = u0 and lie in the range of Φ.

If inhomogeneous Dirichlet boundary conditions are present, then Equation 20-10 is rewritten as

so that y = u − ud is zero on the boundary.

The following reduced matrices can be exported: the mass matrix Em, the damping matrix Dm, the stiffness matrix Km, and the damping ratio matrix

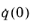
where p = 0, 1, or 2 is the number of columns that were appended to Φ (that is, the damping ratios do not affect the p last diagonal entries). Furthermore, the load vector, ΦHL0; the stiffness matrix times ud, ΦHKud; the projection matrix, Φ; the initial value vector, q(0); and the initial derivative vector, , can be exported.

For a Frequency Response, Modal study (see Frequency Domain, Modal), the load L is assumed to be of the type

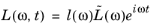where ω is the angular frequency of the forcing function and l(ω) is the given load factor.

The steady-state solution of Equation 20-10 is then of the form

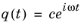
Use the expression of L from Equation 20-13 and the expression of q from Equation 20-14 in Equation 20-12. Since the coefficient matrices can depend on the frequency, expand around the first frequency f0 = ω0/(2π), and truncate after three terms. You then get

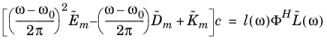
An approximate solution to the original problem is given by um = Φq, but as usual only the time-independent factor Φc is returned. If damping ratios are provided, the term

is added to the sum inside the square bracket of Equation 20-15. Notice that when the coefficient matrices are independent of the frequency, this damping term coincides with what is added in the corresponding Time Dependent, Modal study.

The only type of parameter-dependent Dirichlet boundary conditions that are supported are those that can be written as a scalar frequency-dependent function times a constant vector (that is, the constraint vector M can be written as M = l(ω)M0). For inhomogeneous Dirichlet boundary conditions, a particular solution is needed. To homogenize the original problem, a particular solution up = vp eiωt is computed from the nonreduced equation

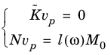
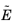
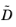
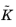
is then subtracted from the right side of Equation 20-15. Here, , , and are the unreduced coefficient matrices from the above expansion around the first frequency. Once an approximate solution, uh, of the homogeneous problem has been found using modal analysis, an approximate solution of the inhomogeneous problem is given by uh + up.

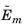
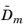
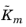
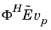
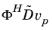
For frequency response studies, the following reduced matrices can be exported: the mass matrix, ; the damping matrix, ; and the stiffness matrix . The damping ratio matrix, Dratio; the projection matrix, Φ; the mass matrix times the particular solution, ; the damping matrix times the particular solution, ;and the load vector 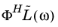can also be exported. The exported load vector is assembled for the last given frequency ω. You can also export all load vectors (that is, , , …, ). 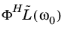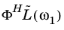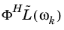This results in a matrix whose columns are all assembled load vectors. 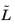If is independent of ω, this matrix only contains one column.