Stationary in the COMSOL Multiphysics Programming Reference Manual
|
Stationary in the COMSOL Multiphysics Programming Reference Manual
|
|
•
|
For Automatic, Sj is the average of |Ui,j| for all DOFs i for fixed j, times a factor equal to 10−5 for highly nonlinear problems or 0.1 otherwise.
|
|
•
|
For Manual, Sj is the value given in the Scale field. Sj is multiplied by a factor equal to 10−5 for highly nonlinear problems or 0.1 otherwise
|
|
•
|
For Initial value based, Sj is the average of |Vi,j| for all DOFs i with fixed j times a factor equal to 10−5 for highly nonlinear problems or 0.1 otherwise. V = U0 is the solution vector corresponding to the initial value. In case all DOFs are zero for that particular field j, the total mean of |Vi,j| for all i and j is used instead.
|
|
•
|
|
The (automatically damped Newton) nonlinear solver only checks the convergence criterion if the damping factor for the current iteration is equal to 1. Thus, the solver continues as long as the damping factor is not equal to 1 even if the estimated error is smaller than the requested relative tolerance.
|
|
•
|
For Automatic, the weights
|
|
•
|
|
•
|
With consistent initialization active, the base residual f and the weights
|
|
•
|
When the weights
|
|
•
|
For wave problems, the weights
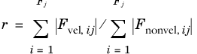 , where F is the current residual. The weights , where F is the current residual. The weights |
|
•
|
Use the linear solver to solve a linearized (nonlinear) problem. See the section about linearity in Stationary Solver for details on how the residual is assembled in this case.
|
|
•
|
The next factor is used to control the CFL number toward the requested target error estimate. A standard local error estimate control uses only a factor of this sort, but for this type of control, the absolute level of the error is not that important. However, without this factor (kI = 0), the CFL number might drift even though the error level is fluctuating on the same level. This factor can also be used to select an absolute regime for the error where increasing the CFL number should be more difficult.
|