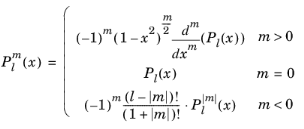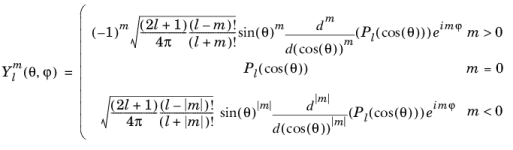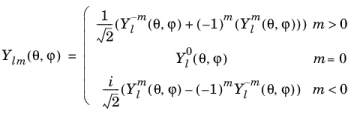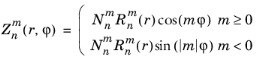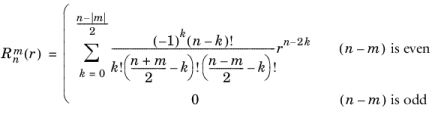The legendre(l,x) function evaluates a Legendre polynomial Pl(x) of integer degree l:

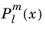
The legendre(l,m,x) function evaluates an associated Legendre polynomial of integer degree l and order m:

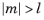
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , legendre(l,m,x) returns zero.

The special power and square root functions poweps and sqrteps, respectively, are needed when the derivatives of expressions need to be evaluated near zero. For example, when evaluating the results of a small-signal analysis and computing the differential during postprocessing. The functions themselves evaluate to the exact value of the or power (^) and square root (sqrt), respectively. Epsilon is only added into the expressions for their derivatives. For an expression poweps(x,n) = a^n, its derivative with respect to x is n·(x+eps)^(n-1). For an expression sqrteps(x) = sqrt(x), its derivative is 0.5/sqrt(x+eps).

The sphericaly(l,m,theta,phi) function evaluates the spherical harmonic function :

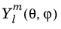
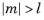
where Pl is the Legendre polynomial of degree l. The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericaly(l,m,theta,phi) returns zero.

The sphericalyr(l,m,theta,phi) function evaluates the real spherical harmonic function :

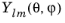
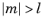
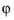
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericalyr(l,m,theta,phi) returns zero. The arguments θ and must be real.

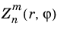
The zernike(m,n,r,phi) function evaluates a Zernike polynomial defined in the following way:

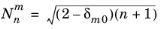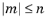
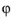
and is the normalization factor. The n argument is required to be a nonnegative constant integer, and the m argument is required to be a constant integer satisfying . The r and arguments are required to be real.