You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Large Eddy Simulations offer an alternative approach to turbulent flow simulations as compared to the RANS approach (see Theory for the Turbulent Flow Interfaces). In LES, the larger three-dimensional, unsteady eddies are resolved, whereas the effect of the smaller eddies is modeled. This requires the simulations to be three-dimensional and time dependent. The current implementation of the LES interfaces is suitable for incompressible flow only. The velocity and pressure fields are divided into resolved and unresolved scales. Denoting the fields containing all scales with capital letters, the decomposition can be expressed as
(3-155)
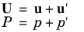
Inserting Equation 3-155 into the incompressible form of the Navier–Stokes equation and the continuity equation yields
(3-156)
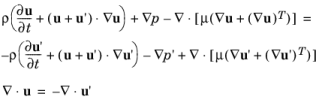
Next, Equation 3-156 is projected onto the finite element sub-spaces of the resolved velocity and pressure scales. Denoting the test functions for these scales by
v and
q, respectively, the projection can be expressed as
(3-157)
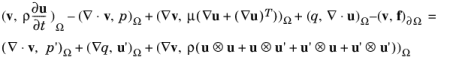
In Equation 3-157,
f is the applied traction force on the boundary
∂Ω of the spatial domain
Ω, and the stresses in the last term on the right-hand side are the resolved nonlinear advection term, the two cross-stresses, and the Reynolds stress. By assuming that the unresolved scales are orthogonal to the inner-product space of the resolved scales, the unresolved time derivative and viscous terms vanish. Another assumption made in the derivation of
Equation 3-157 is that
u' vanishes on
∂Ω (see
Ref. 1 for further details).
(3-158)
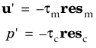
(3-159)
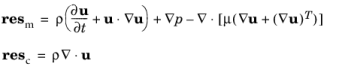
(3-160)

Here, C1 is a constant depending on the temporal scheme,
C2 a constant depending on the shape of the element, and
C3 a constant depending on both the order of the shape functions and the shape of the element.
G is the covariant metric tensor. When the
Use dynamic subgrid time scale option is selected, the first term under the square-root in
Equation 3-160 is replaced by an estimate of the time-derivative based on the resolved scales.
In certain cases, the residual-based Reynolds-stress contribution has been found to be too small (see Ref. 2). For this reason, the Residual Based Variational Multiscale with Viscosity (RBVMWV) method adds a residual based viscosity term to the right-hand side of
Equation 3-157,
(3-161)
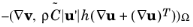
where 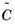 is a model constant, and h
is a model constant, and h is a measure of the element size.
(3-162)

(3-163)
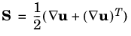
and 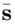 is the projection of S
is the projection of S onto the space of constant shape functions. This corresponds to a further decomposition of the resolved scales into large resolved scales and small resolved scales, in which only the latter are affected by the Reynolds stress (see
Ref. 3). Since the term,
Equation 3-162, identically vanishes for linear shape functions, the
Dicretization must be set to at least
P2-P2 in order to include the Reynolds stress contribution in the Smagorinsky model (see
Discretization).
When Wall treatment is set to
Low Re, a Dirichlet condition is imposed on the velocity field at the walls. Adequate resolution of the wall layers requires that
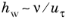
, where
hw is the thickness of the mesh cells next to the wall and
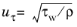
is the friction velocity based on the tangential stress
τw at the wall.
When Wall treatment is set to
Automatic, a Dirichlet condition is imposed on the wall-normal velocity component and a traction force is applied in the tangential direction opposite to the local velocity vector. To evaluate the magnitude,
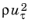
, of the traction force, the Reynolds number based on the magnitude of the tangential velocity and the normal distance,
y, to the wall,
is evaluated halfway between the wall and the first vertexes inside the domain, at y = δw. Asymptotic solutions to the L-VEL equation (
Equation 3-75) can be found for low and high values of the Reynolds number. For low values of the Reynolds number (inside the viscous wall layer),
The Automatic option should be used with caution since boundary layers, especially on smooth surfaces, in many cases need to be resolved down to the top of the viscous wall layer (
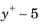
). When the point of boundary-layer separation is known, such as for the flow around bodies with sharp edges, the
Automatic option may be used to reduce the number of DOFs in the model.
where hU is the mesh size in the streamline direction. Larger values of
Δt may lead to damping of turbulence and in some cases even convergence issues. The built-in variable
spf.dt_CFL may be used to limit the maximum time step.